KAPPA DDA Book v5.12

84 / 743

Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017 Chapter - p84/743
The Levitan method addresses the main limitation of the von Schroeter et al. method.
However two problems remain:
a) It requires a re-iterative process where the initial pressure is assessed and corrected
until the coherence of all convolutions is reached. Attempts to add an optimization loop
on pi have failed so far.
b) A deconvolution using a given build-up and a single additional point (the initial
pressure) will not provide additional, intermediate behaviors that we may detect if we
were running a single optimization on all build-ups. Some information is therefore
potentially lost in the separation process.
3.D.4 Deconvolution Method 3 (Houzé et al., 2006-2010)
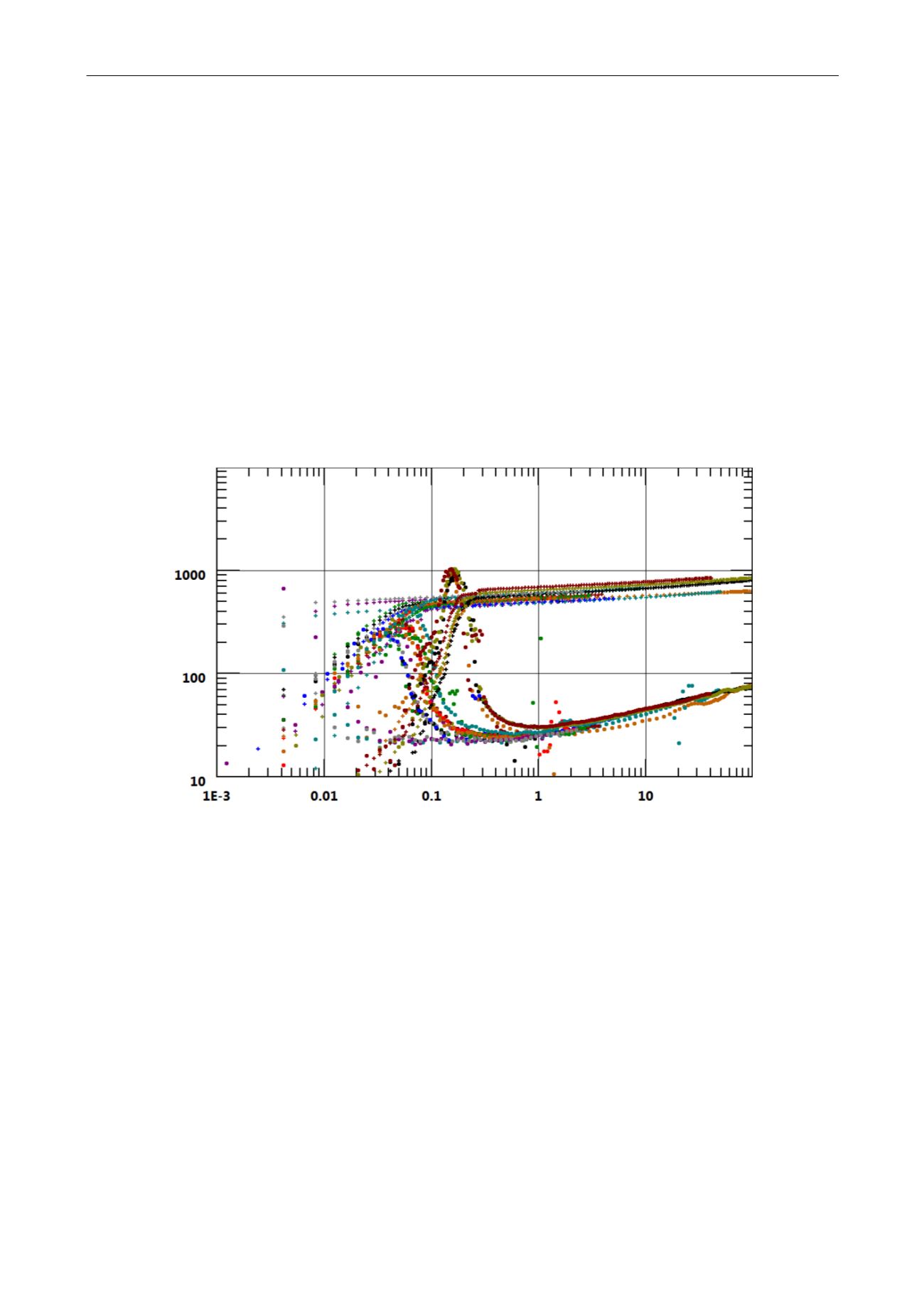
When we extract several shut-ins from PDG data and compare them together on a rate
normalized loglog plot, they often, remarkably exhibit the same behavior at late time but
vastly differ at early time, with different wellbore behaviors and apparent skin factors.
Fig. 3.D.18 – Multiple build-ups from PDG data
This inconsistency ruins the stability of the von Schroeter et al. method and forces the
engineer to go into the tedious process of trial and error of the Levitan method.
When the inconsistency comes from different behavior at early time, a solution is proposed.
To illustrate this we can run a very simple simulation, or test design, of two systems with
different wellbore storages and skins but the same reservoir / boundary model. In this
example we use the simplest homogeneous infinite behavior but it applies to more complex
systems. The loglog plot of both responses is shown below left. Simulation 1 has a constant
wellbore storage. Simulation 2 has a larger, changing wellbore storage and a higher skin
value.
The plot below right compares both simulations on a linear scale and displays the difference
between them. During the production phase, the simulations differ with an early time transient
corresponding to the different wellbore effects and the skin. When wellbore effects fade the
difference stabilizes at a level corresponding to PSkin(Skin). When the well is shut-in there is
again a transient behavior, but when the wellbore effect fades the difference stabilizes to zero.
We will call this limit time the convergence time.