
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapter
3 – P ressure Transient Analysis (PTA)- p85/743
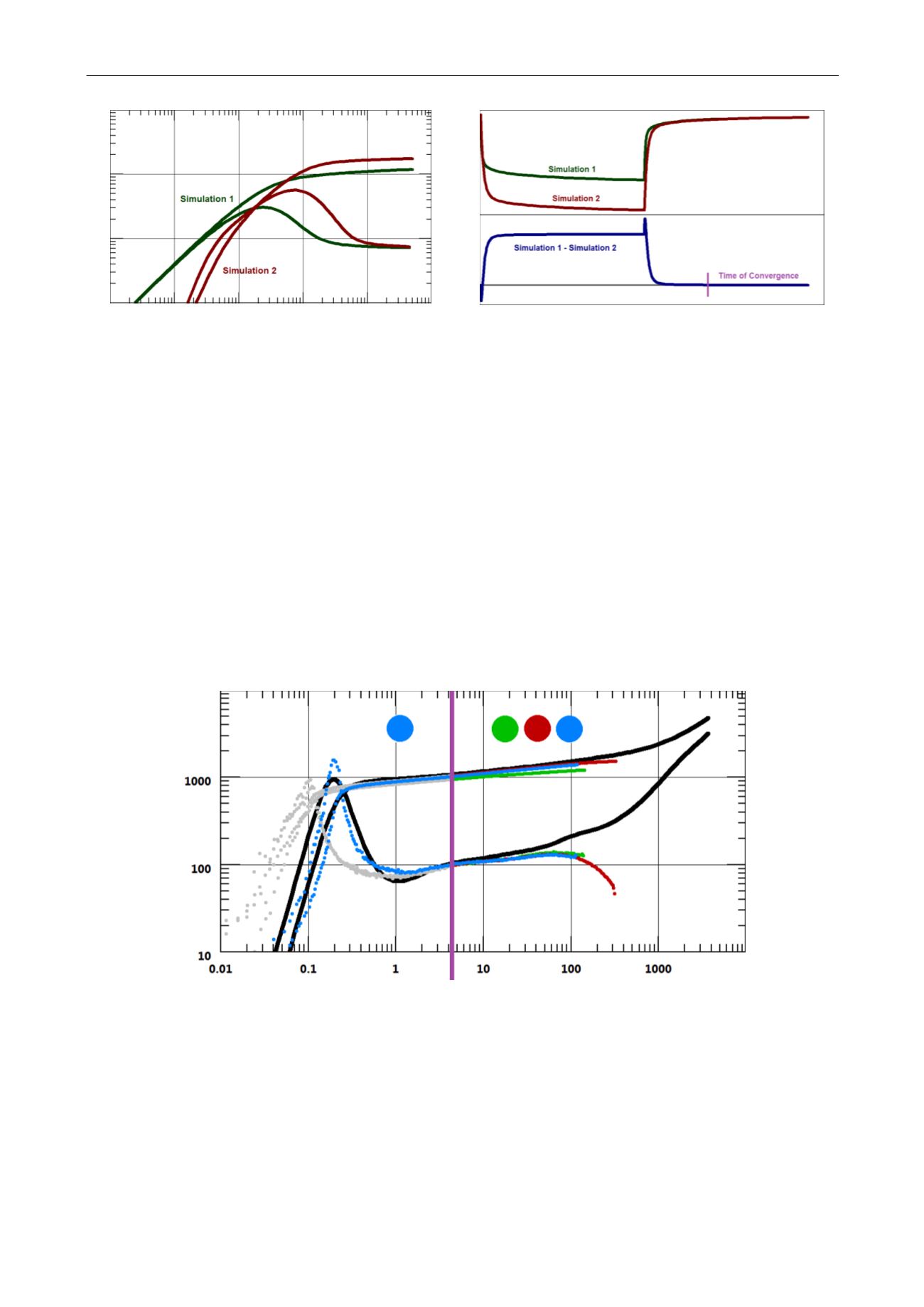
Fig. 3.D.19 – Two simulations: log log plot
Fig. 3.D.20 – Two simulations: linear plot
On the loglog plot, pressures do not merge at late time because we are plotting
P(
t) = P
Shut-
in
(
t) – P
wf
(
t=0). The P
Shut-in
values converge, and
P stabilizes at P
wf1
- P
wf2
The deconvolution is an optimization on P, not
P. We will get a stable process, not affected by
early time discrepancies, if we run an optimization on one build-up and the last part of the
other build-ups after convergence.
The Houze et al. method (called ‘Deconvolution on one reference period and the end on the
other periods’ in Saphir), allows specifying which period (blue in our case) will be taken as a
reference and all its data taken into account and the other periods (green and red) will be
taken into account at late time after the convergence time specified by the user.
It gives a single deconvolution matching with the reference period early time and
corresponding to all the periods at late time as shown below:
Fig. 3.D.21 – Deconvolution with a period reference early time
and all periods late time
3.D.4.a
Variant 1: Using Levitan method after Method 3
The main variable in the Levitan method is the initial pressure. Method 3 brings a value for pi
which is meant to be compatible with all selected build-ups and is a good candidate for the
Levitan method. Without any engineer interaction, the initial pressure resulting from Method 3
is used to execute the Levitan method immediately after Method 3, with no more trial-and-
error.
















