
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapter
3 – P ressure Transient Analysis (PTA)- p79/743
)
ln(
t
and
d
dp
t
d
t
dp
z
u
u
) (
ln
)
ln(
) (
ln ) (
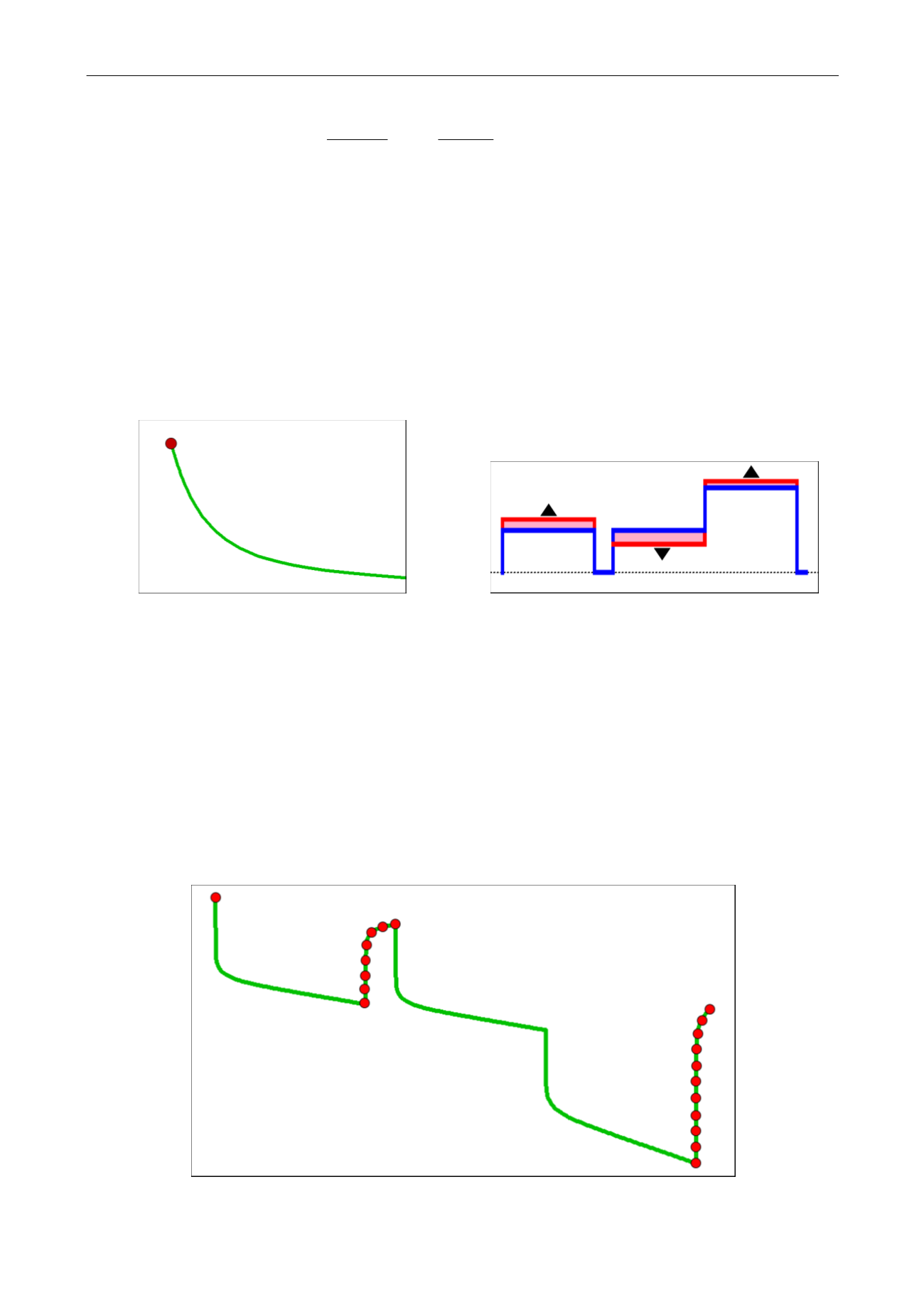
The principle of the new deconvolution method is to find the derivative curve z(
) which, using
a modified convolution expression, will match the data. The curve z(
) is defined as a polyline
or a spline. It has an initial point, as (0,0) makes no sense on a loglog scale. Its time range is
the elapsed time between the beginning of the production history and the last data point we
will try to match (3,200 hr in the previous example).
The curve z(
) is the main unknown. There are two additional sets of optional unknowns: the
first is the initial pressure p
i
, which may or may not be known. The last unknown is a tolerance
to errors in the rate history, which we need to introduce for the optimization process to
converge.
Fig. 3.D.6 – 2
nd
unknown: p
i
Fig. 3.D.7 – 3
rd
unknown:
q’s
3.D.2.b
Problem objective function
The three unknowns above are adjusted, in a nonlinear regression process, to minimize an
objective function. This objective function has three components.
Naturally, the first and main component of the objective function we want to minimize is the
standard deviation between the convolved model and the pressure data
(Fig. 3.D.8below).
This may be all pressure data or, more likely, a series of time intervals where the pressure
data is considered reliable. Typically, successive build-ups are a good candidate, unless the
producing pressures are exceptionally smooth as in the case of clean gas tests for example.
Fig. 3.D.8 – 1st objective function
minimize distance between simulated and real data
















