KAPPA DDA Book v5.12

80 / 743

Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017 Chapter - p80/743
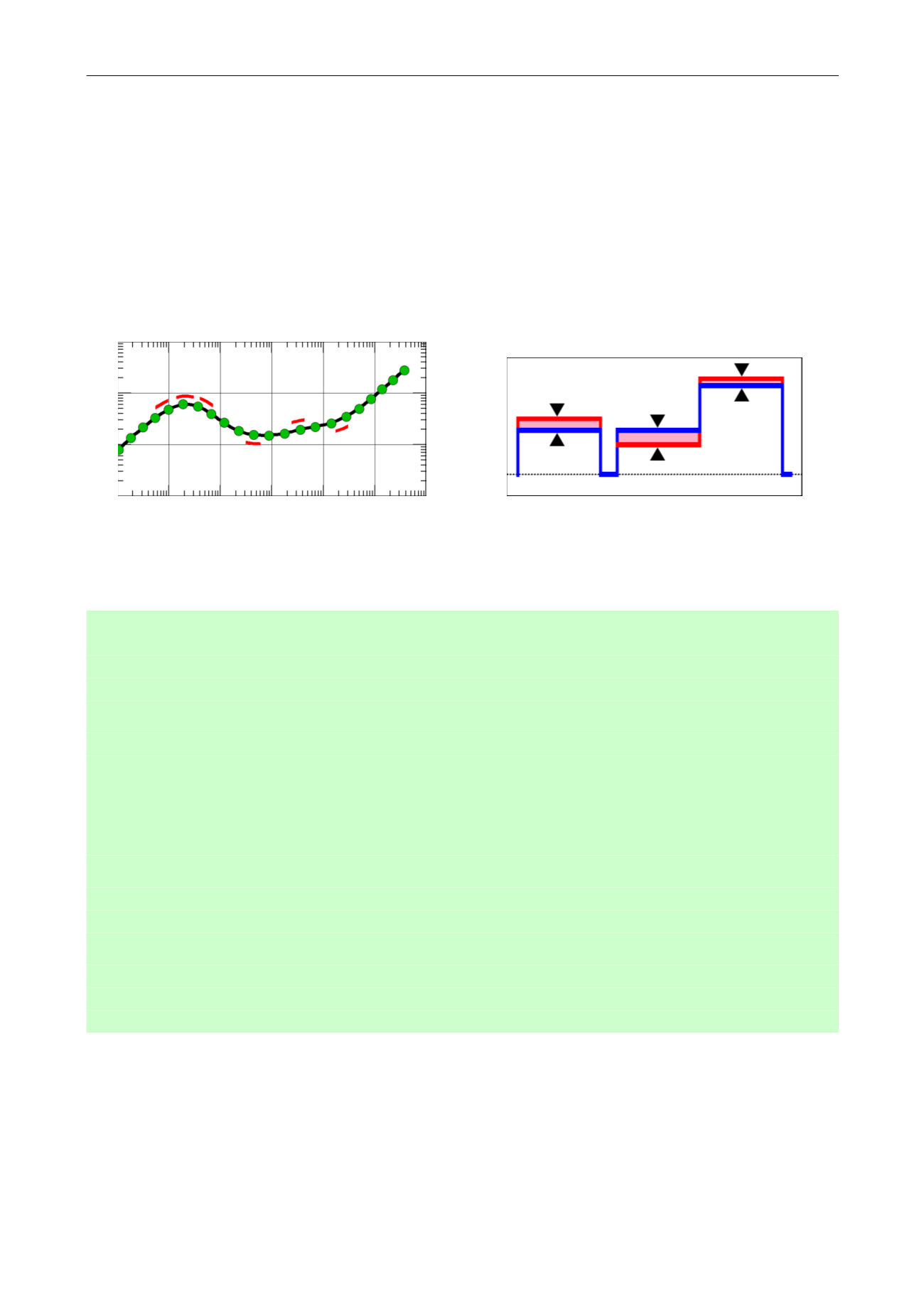
The second component of the objective function is the total curvature of the derivative
response. When several derivative responses provide an equivalent match, the idea is ‘the
simpler the better’. Among the candidate responses, the one with the smallest total curvature
is selected. In other words, if several variations give a good fit, the one that transits smoothly
between the points is preferred to those that oscillate.
The third and last component of objective function is the modification in the rate values
required to obtain a match. Again, for the same quality of match, the solution that requires the
smallest changes in the rates is selected.
Fig. 3.D.9 – 2nd objective function
minimize total curvature
Fig. 3.D.10 – 3rd objective function
minimize rate correction
3.D.2.c Deconvolution in plain English
This essence of this new deconvolution method is optimization. Instead of optimizing model
parameters at the end of the interpretation, we take a discrete representation of the derivative
we are looking for, and we shift it and bend it until it honors the selected data after
integration, to give us a unit pressure change response from the derivative, and convolution,
to take the rates into account.
Because we need to account for some uncertainties on the rates and for better behavior of the
optimization algorithm, we allow the rates to change a bit, but we try to make this change as
small as possible.
We want the resulting derivative curve to have the same kind of signature as the various
analytical and numerical models we use. To achieve this we make sure that the total curvature
of the response is reasonable, i.e. the resulting curve is not too twisted.
Once we get our deconvolved derivative, we integrate to get the pressure response and show
both pressure and derivative on a loglog plot. As this is the theoretical response for a constant
rate, we match the deconvolved data with drawdown models, not superposed models.
Because this deconvolved response is not data, but ‘only’ the result of an optimization that
may be imperfect, we keep an eye on the real data by superposing the model and looking at
the history match on the real, not the deconvolved signal.
3.D.2.d Field data application
The history plot below shows 3,000 hours of permanent pressure and rate recordings. The
three longest build-ups are extracted and shown on a loglog scale below.
The green and red build-ups are strictly telling exactly ‘the same story’, while the blue build-up
is consistent at late time but diverges at early time, with apparently a different wellbore
storage and skin.