
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapter
3 – P ressure Transient Analysis (PTA)- p83/743
As deconvolution can be done using pi and any build-up, the idea of the Levitan method is to
perform one deconvolution for each build-up with a common value of initial pressure. The first
guess of pi may produce divergent deconvolution responses. The value of pi is reiteratively
changed until one gets a consistent late time response for all deconvolutions. Because each
deconvolution only honors one build-up data at a time, there will not be any instability at early
time.
This process is easily accessed in Saphir: this Levitan et al. deconvolution method is proposed
when multiple periods are extracted: ‘Separate deconvolutions with a common pi’ (Levitan et
al). The checkbox ‘force Pi to:’ is automatically tagged ‘on’ and pi must be entered manually.
This option calculates automatically one deconvolution per extracted period. The results
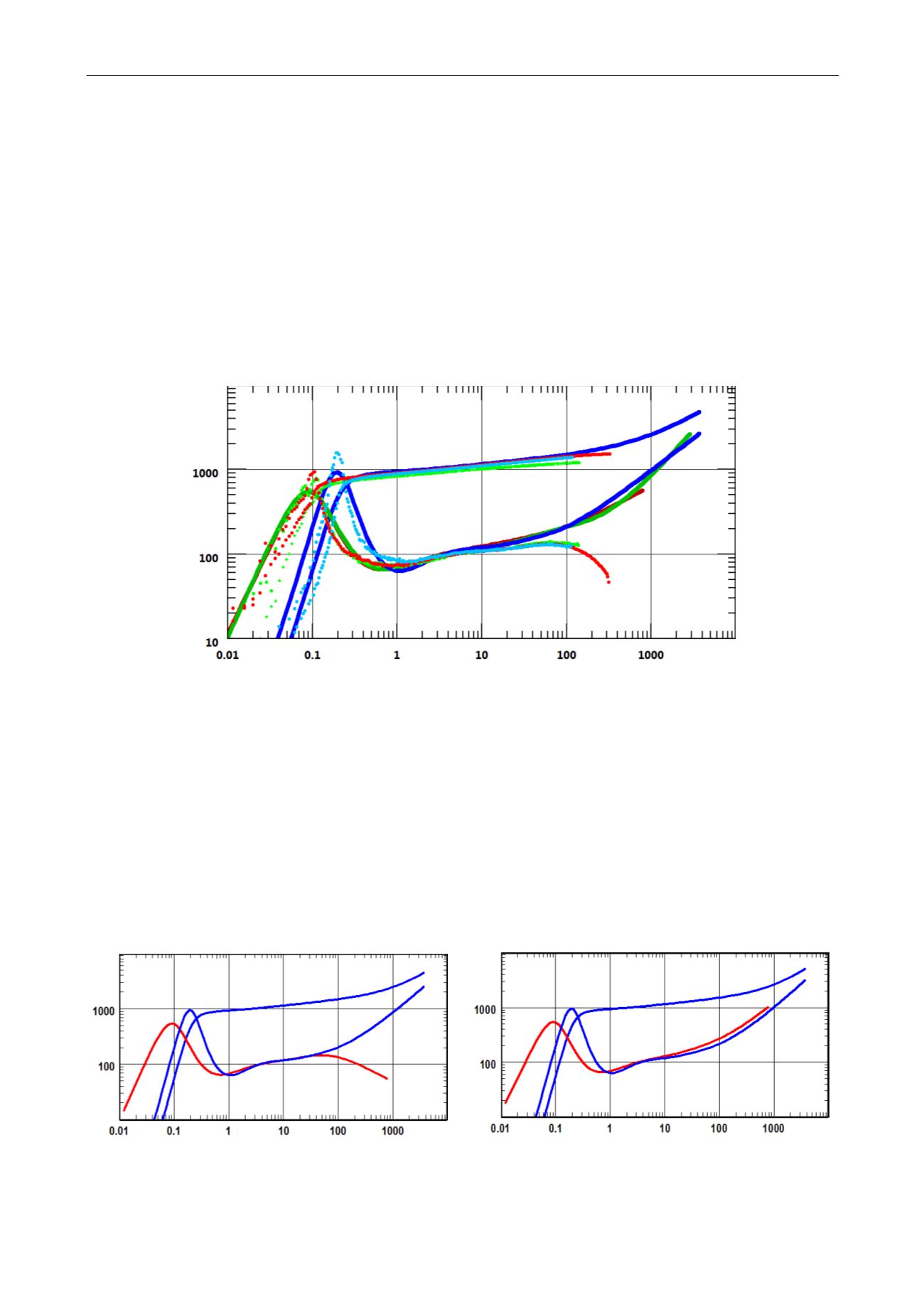
working on the 3 build ups is shown below:
Fig. 3.D.15 – Automatic ‘separate deconvolution with a common pi’
When ignoring the Pi:
The process would be a bit more complicated if we did not have a couple of coherent build-ups
to start with. If we had, say, only Build-up #1 and Build-up #3, we would have to ‘play’ with
the initial pressure until the late time behaviors are coherent and give the same reservoir size.
Attempts at deconvolution with values that are both too low too high for pi are shown in the
plots below.
This becomes a trial-and-error process, until the late time behavior is coherent for the two
build-ups although this just may not be possible. We see on the plots below that the late time
behavior are reasonably coherent but crossing each other.
Fig. 3.D.16 – Separate deconvolutions
initial pressure too low
early build-up ‘below’ late build-up
Fig. 3.D.17 – Separate deconvolutions
initial pressure too high
early build-up ‘above’ late build-up
















