
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapter
3 – P ressure Transient Analysis (PTA)- p81/743
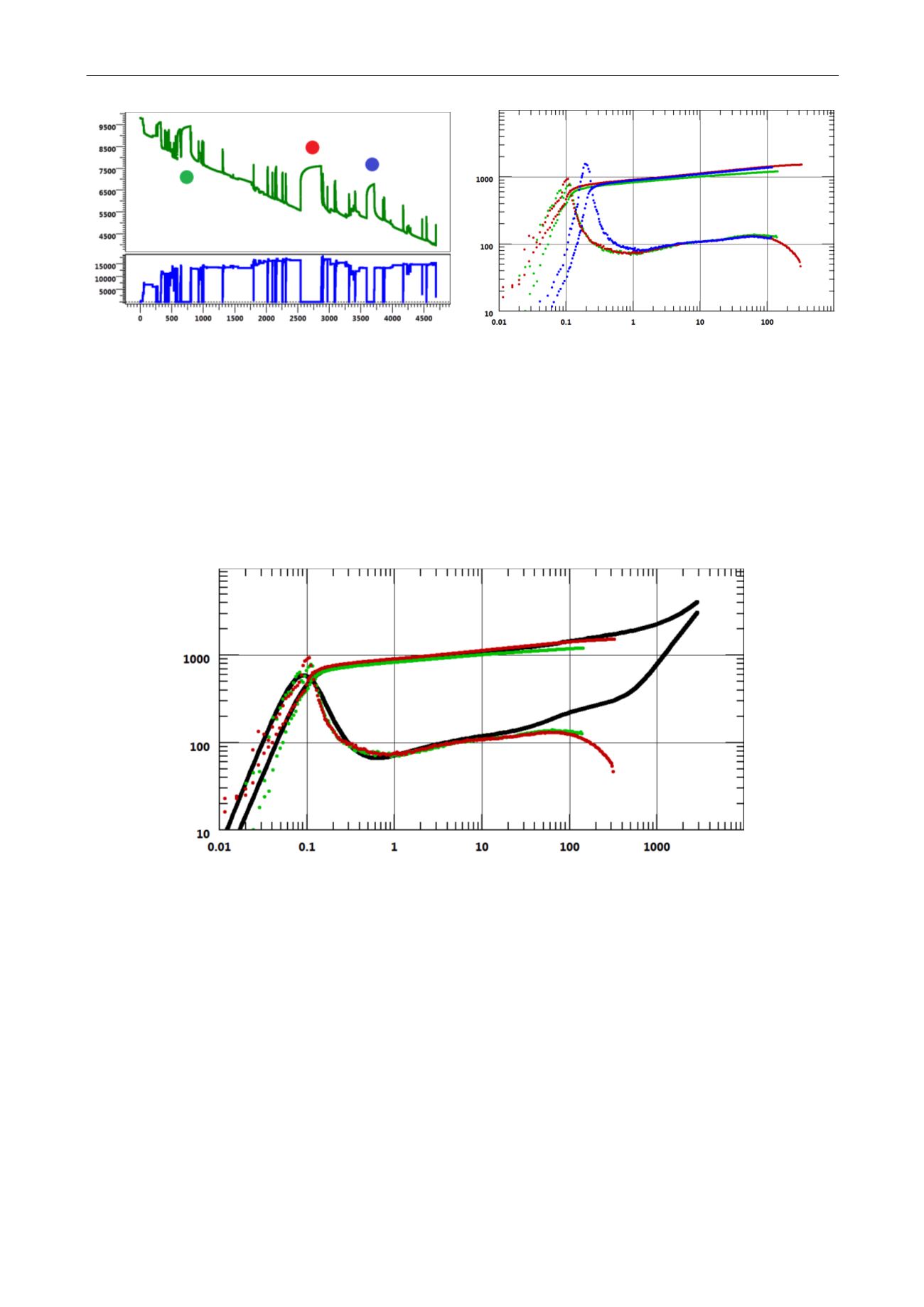
Fig. 3.D.11 – Production and pressure history
Fig. 3.D.12 – Normalized loglog plot
If we apply the von Schroeter et al. method on the two coherent build-ups (green and red) the
process is successful and the resulting deconvolution is shown in the figure below. The late
derivative dip in both build-ups does not correspond to a pressure support but the beginning of
a closed system. The late time unit slope in the deconvolution derivative will provide a fair
estimate of the well drainage area. Because we had two build-ups the deconvolution process
could also back calculate a consistent value for the initial pressure.
Fig. 3.D.13 – Deconvolution with the two consistent BU’s
3.D.2.e
Main limitation of von Schroeter et al. method
We take the same real example as in the previous section, but we consider the third build-up
later in the same well production history. If we extract and compare the derivative response of
the three build-ups, they tell more or less the same story at late time but the early time
response is inconsistent with the two initial build-ups.
If we calculate the convolution with no constraint from the three build-ups, or even using any
of the two first build-ups and the last, we get an erratic deconvolved signal (see figure below).
Coming back to Earth, we should remember that deconvolution is, after all, only a nonlinear
regression process.
















