KAPPA DDA Book v5.12

Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017

Chapter

- p90/743

One element of answer is to calculate a sensitivity. The deconvolution parameters include the

points of the z(



) response, the curvature of this response and the rate changes. Looking in

the Jacobian of the deconvolution matrix we can see the sensitivity of the match to the

individual points of the z(



) response. In Saphir we normalize this and show it as a vertical

sensitivity band for each point of z(



This band does not quantify the real, physical, uncertainty. It only provides a blunt statistical

description of the problem around the solution point and answers the question, “By how much

can I move this node until the match is affected?” If the sensitivity is high, we are close to

positive information and the uncertainty band is narrow. If, on the contrary, moving a point up

and down has no or little effect on the global response, then we know that this section of the

response may not be very relevant. In order to illustrate this we have taken two extreme

examples.

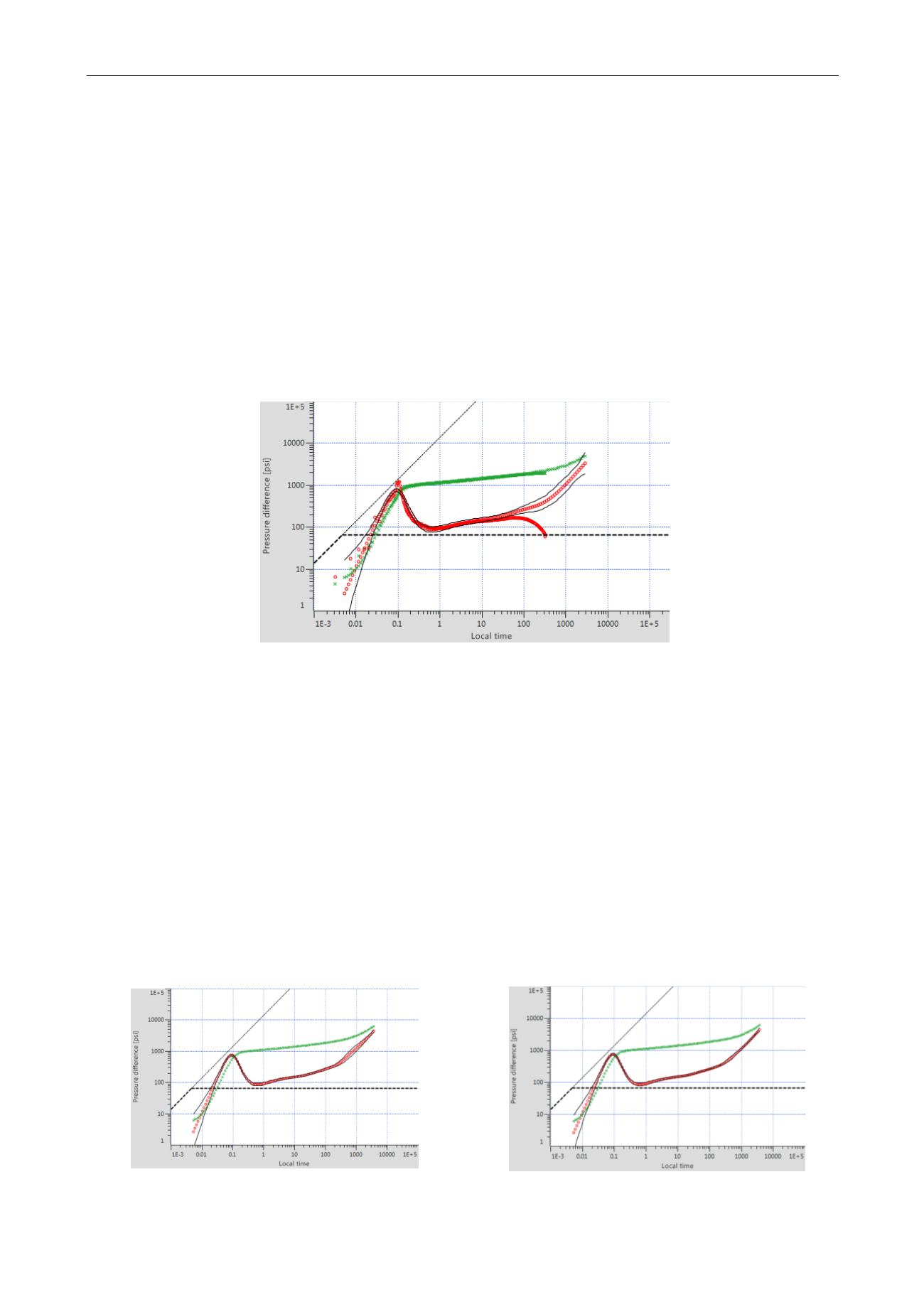
Fig. 3.D.28 – Sensitivity representation

single build-up and no pi (1/2)

In the above figure we have done what we should never do: calculate a deconvolution with a

single build-up WITHOUT imposing a value of pi. The problem is completely under-defined,

because we can move the tail end of the deconvolution and get a perfect match of the data by

compensating pi. So the tail end is completely irrelevant and it shows on the sensitivity plot.

In the below left figure, we have run the deconvolution with the two build-ups of the original

example. We let pi be calculated by the deconvolution process. As one can see, the sensitivity

is much better, but intermediate behavior could have been different. What made the

deconvolution pick the selective curve was its smoothness. Now, in the right side figure the

same deconvolution was run but the value of pi was fixed. This makes the sensitivity graph

even better.

Fig. 3.D.29 – Sensitivity representation

two build-ups and no pi

Fig. 3.D.30 – Sensitivity representation

two build-ups and pi