
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapter
3 – P ressure Transient Analysis (PTA)- p77/743
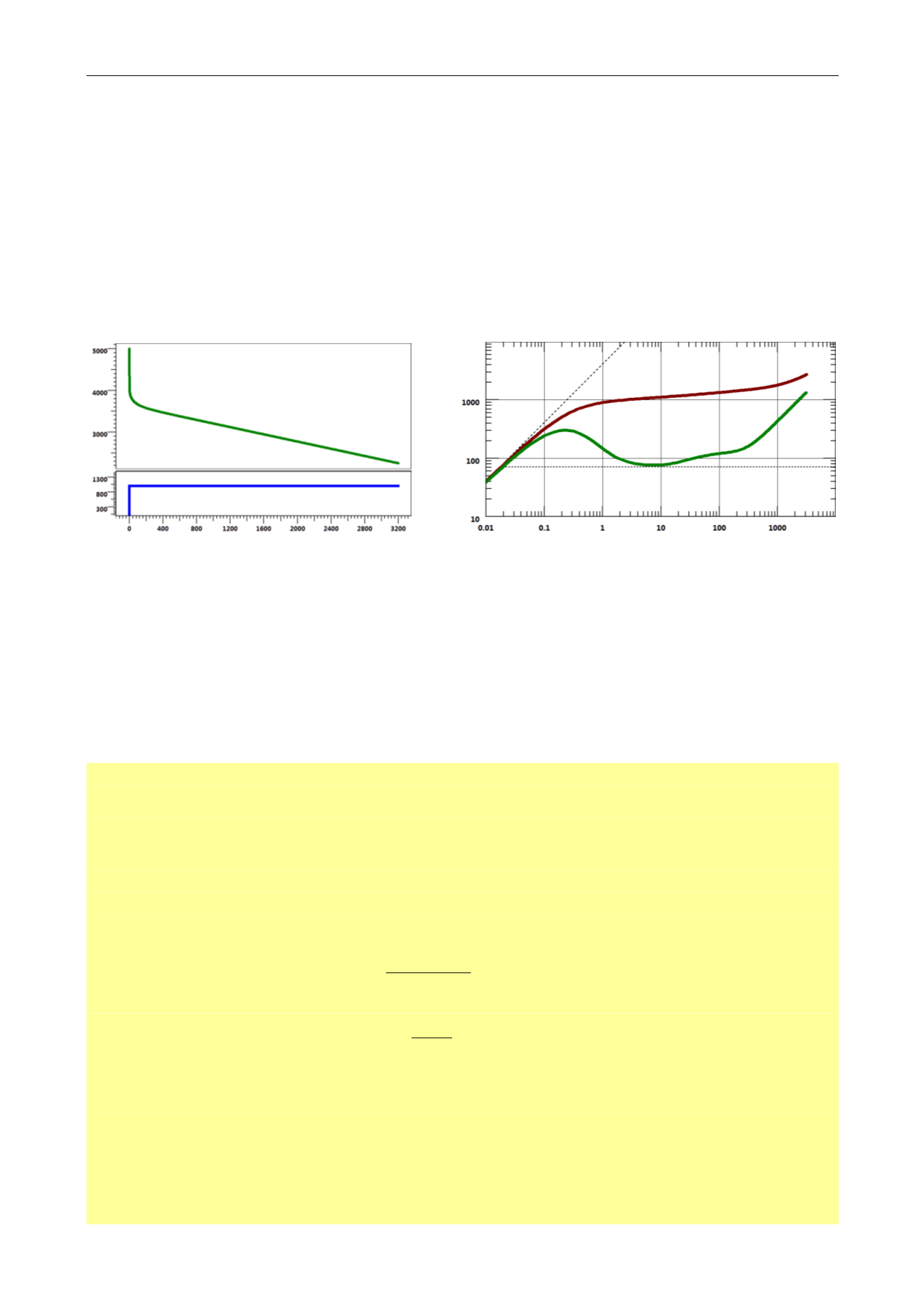
The idea behind deconvolution is, in this example, to recreate from the real data, the ideal
pressure response to a constant production over the same period (see below). If such a
response was created, we could extract a loglog response of 3,200 hours duration, and the
virtual data extracted this way would show much more of the reservoir than the 100 hour
build-up could possibly reveal alone.
In other words, if we extract the deconvolved data from the real pressure response without
assumptions, we will be able to get a much longer response, or the same response for a much
shorter test.
Fig. 3.D.3 – Deconvolution: p
u
(t)
Fig. 3.D.4 – Deconvolution:
p
u
(
t) &
p’
u
(
t)
In theory we may not even need to shut the well in. With deconvolution we would make a
stepwise construction of an ideal constant pressure response and be able to perform a
Pressure Transient Analysis whenever we have some rates and pressures recorded at the same
time. One of the Holy Grails of transient analysis has been found?
3.D.1.b
Mathematical formulation
Before looking at deconvolution, we need to know a little about what constitutes convolution.
The mathematical definition of the convolution of two real functions is:
t
d tg f
tg f
0
)(
Convolution is what we do when we apply the principle of superposition (see Chapter 2) in
order to get the pressure response
p(t) for a complex rate history q(t) knowing the ideal
pressure drop
p
u
(t) for a constant, unit production. We have:
d t p q d
t
tp
q t p
t
u
t
u
w
0
0
)
('
)(
)
(
)
(
)(
)(
Where
t
p
t p
u
u
)( '
In other words:
u
u
p q p qp
'
'
Note that, when the rate history is a step function, the calculation of this integral will bring the
‘usual’ superposition equation, seen in Chapter 2:
i
u
n
i
i
i
i
t tp q q
p tp
1
1
















