
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapter
3 – P ressure Transient Analysis (PTA)- p72/743
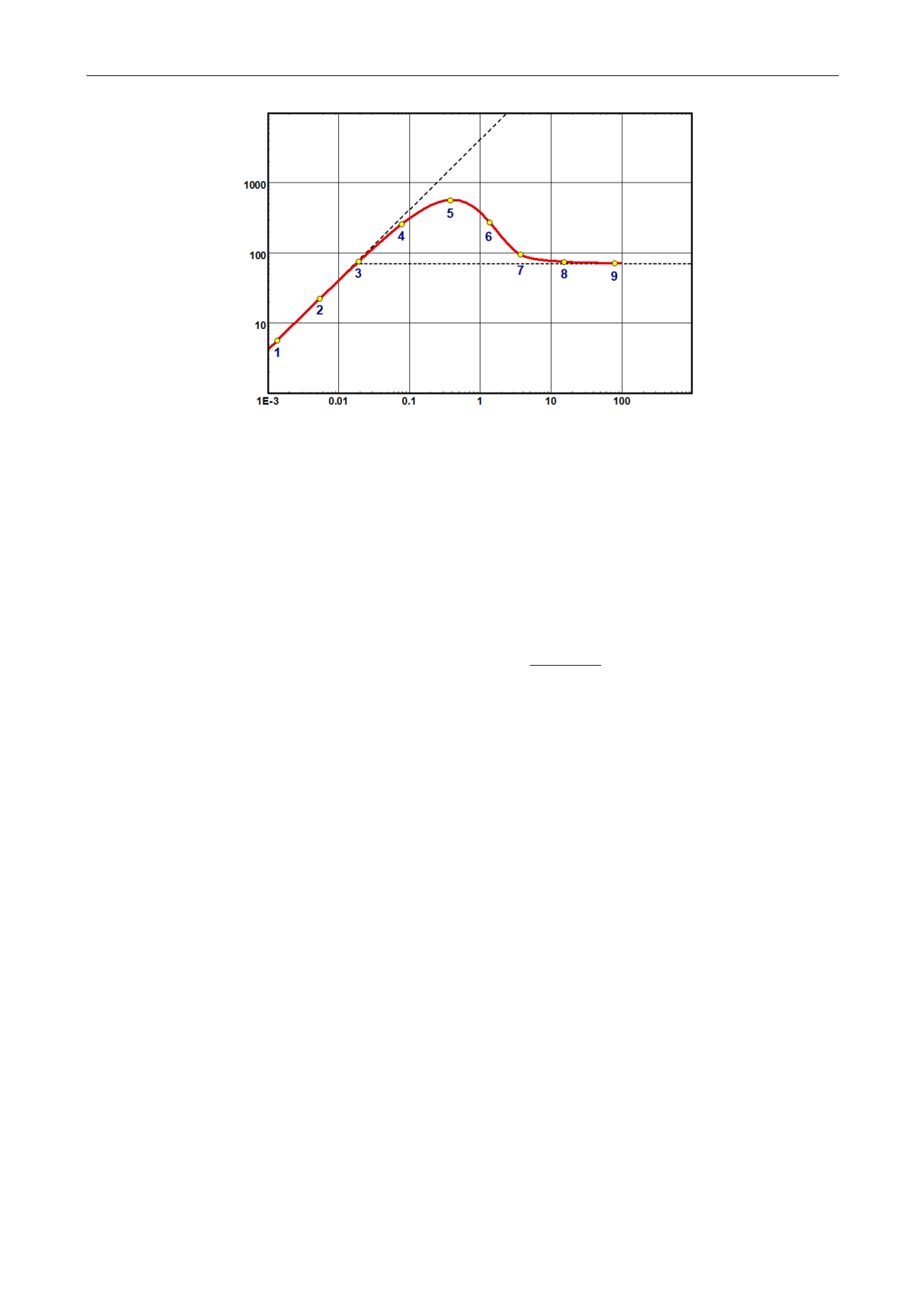
Fig. 3.C.2 – Bourdet derivative, loglog plot
3.C.3
Bourdet Derivative & Infinite Acting Radial Flow (IARF)
When IARF occurs we have the approximation:
t
mp
sup '
Where m
’
is the slope of the semilog straight line. In the following the drawdown response is a
specific case of the multirate response, and the logarithm of time is the specific superposition
time for a drawdown. The derivative is therefore:
Derivative when IARF has been reached:
'
sup
'
m
t
d
pd
p
When IARF is reached, the derivative stabilized to a level equal to the slope of the semilog
straight line. This property was the main reason for the development of the derivative, as it is
easy and straight forward to identify IARF on the loglog plot, something which is virtually
impossible on the semilog plot. One can say that the derivative is a ‘magnifying glass’
of the
semilog behavior, conveniently placed on the same plot, used historically for type-curve
matching.
Combined with the early time unit slope during wellbore storage, the derivative provides an
immediate way to define the pressure and the time match on the loglog plot, just by
positioning a unit slope line on the wellbore storage regime and positioning the horizontal line
on the IARF response.
This alone would have made the Bourdet derivative a key diagnostic tool. The delightful
surprise was that the derivative could do much more, and that most well, reservoir and
boundary models carry a specific signature on the derivative response. It is this remarkable
combination that allowed the derivative to become
THE
diagnostic and matching tool in
Pressure Transient Analysis.
















