
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 3 – P ressure Transient Analysis (PTA) -p100/743
3.E.9
Model refinement
Modification of the parameters: Before leaving the parameter refinement to an optimization
routine, the engineer should deal with the gross parameter errors if there are any. This will
increase the chance for the regression to succeed and converge faster, and it will secure the
choice of the model. Software will generally provide facilities to ease this process. For
example, parameters may be corrected if the engineer shifts the match on the loglog plot.
However, an experienced interpretation engineer with a good understanding of the sensitivity
to the model parameters will often do it faster by changing the values by hand.
Nonlinear regression: The principle is to use numerical optimization to refine the parameter
estimates by minimizing an error function, generally the standard deviation between the
simulated pressures and the real pressures at carefully selected times. The derivative may also
be integrated in the error function. The most commonly used optimization algorithm is
Levenberg-Marquardt, but there are many variants.
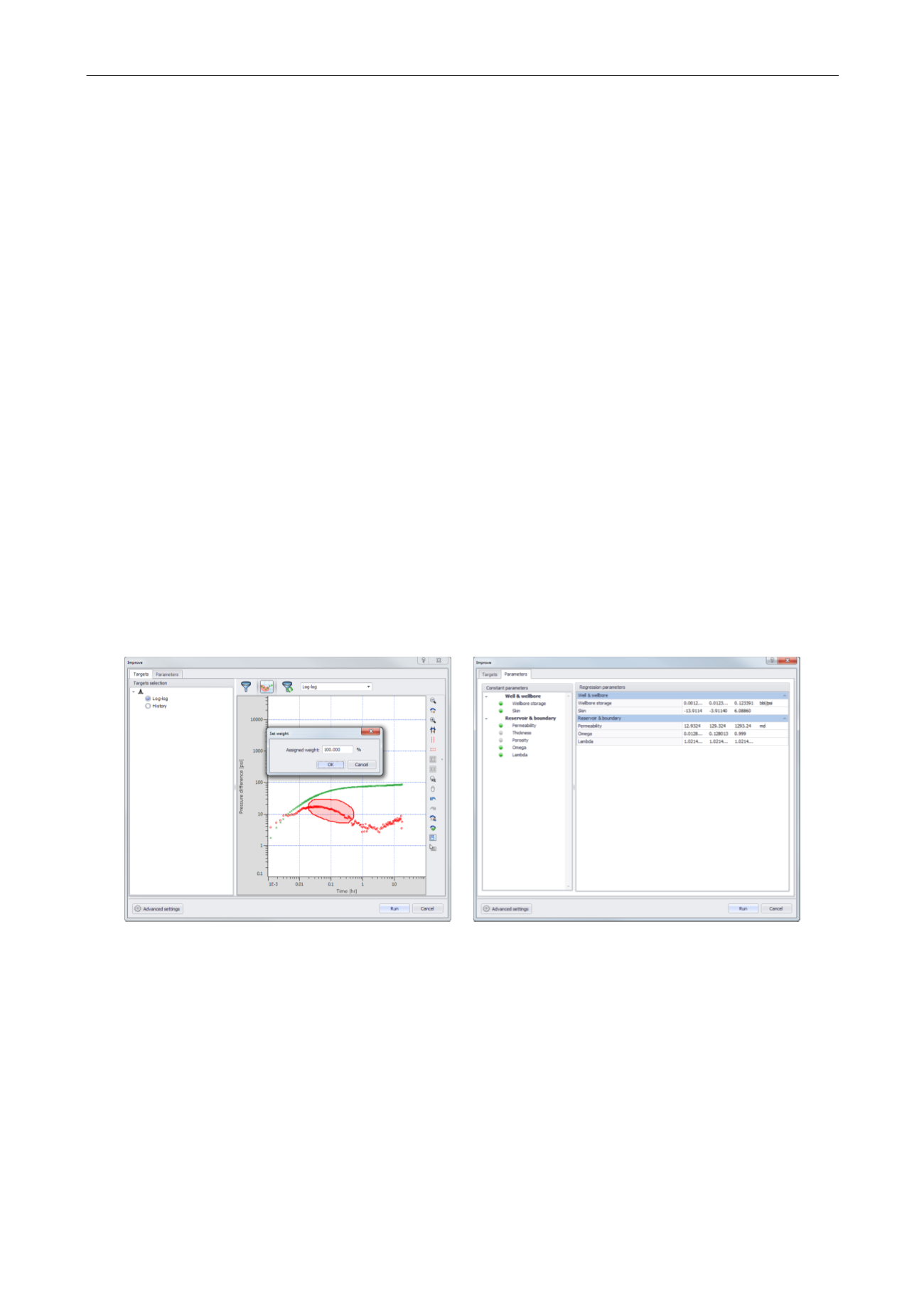
Among the model parameters, some may be fixed by the engineer. For the others, the
engineer may control their upper and lower limits. The data points on which the error function
will be calculated may also be user controlled. One major choice will be whether the
optimization is restricted to the analyzed period, or if it is extended to data outside the
analysis. In the first case, the match at the end of the optimization process will be as good as
or better than the starting point. If the optimization is performed on points beyond the
analyzed period, the overall history match will be improved, but potentially at the expense of
the quality of the match on the period used for the diagnostic.
Fig. 3.E.12 – Setting weight to the regression points and controlling the optimization bounds
3.E.10
Sensitivity study
At the end of the nonlinear regression it is also possible to recover the confidence intervals.
They can be used to assess the sensitivity to individual parameters and eventual parameters
cross-correlations.
One can also run and display series of model generations corresponding to different values of a
given parameter in order to compare them on a single loglog plot. This is, to a certain extent,
the modern version of the type-curves, where dimensionless drawdown solutions are replaced
by the generation and extraction of detailed models with user preset ranges of parameters.
The figure below shows the sensitivity to the distance between a well and one single sealing
fault.
















