
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 2 – T heory- p49/743
…and if we re-shuffle it a bit again, without worrying about calculating a few constants,
including the value of the shape factor for a circle, we get:
kh
er
r
a
qBa
chr
t
qBa tp
Skin
w
e
t
e
ln
ln
2
2
3
2
2
1
Or…
e
Skin
w
t
pore
r
kh
er f t
c V
qBa tp
,
,
1
1
One can see that the slope is a function of the porous volume times the compressibility, while
the constant term is a function of all the transients that happened before PSS occurred.
2.H.5
Effect of errors on the different input parameters
What we have seen so far is the sensitivity of a test / production design on the different
parameters. In the case of a real analysis we will input the ‘known’ parameters, calculate the
model response and vary the ‘unknown’ parameters until the model matches the measured
response. This will ‘calculate’ the ‘unknown’ parameters.
What we will do now is consider that the truth is our reference case. From this reference case
we will change one of the ‘known’ parameters to a wrong value, off by, say, 10%. Then
optimize the model by varying the ‘unknown’ parameters to match the reference case and see
how this affects these parameters (the results from Pressure Transient or Production
Analyses).
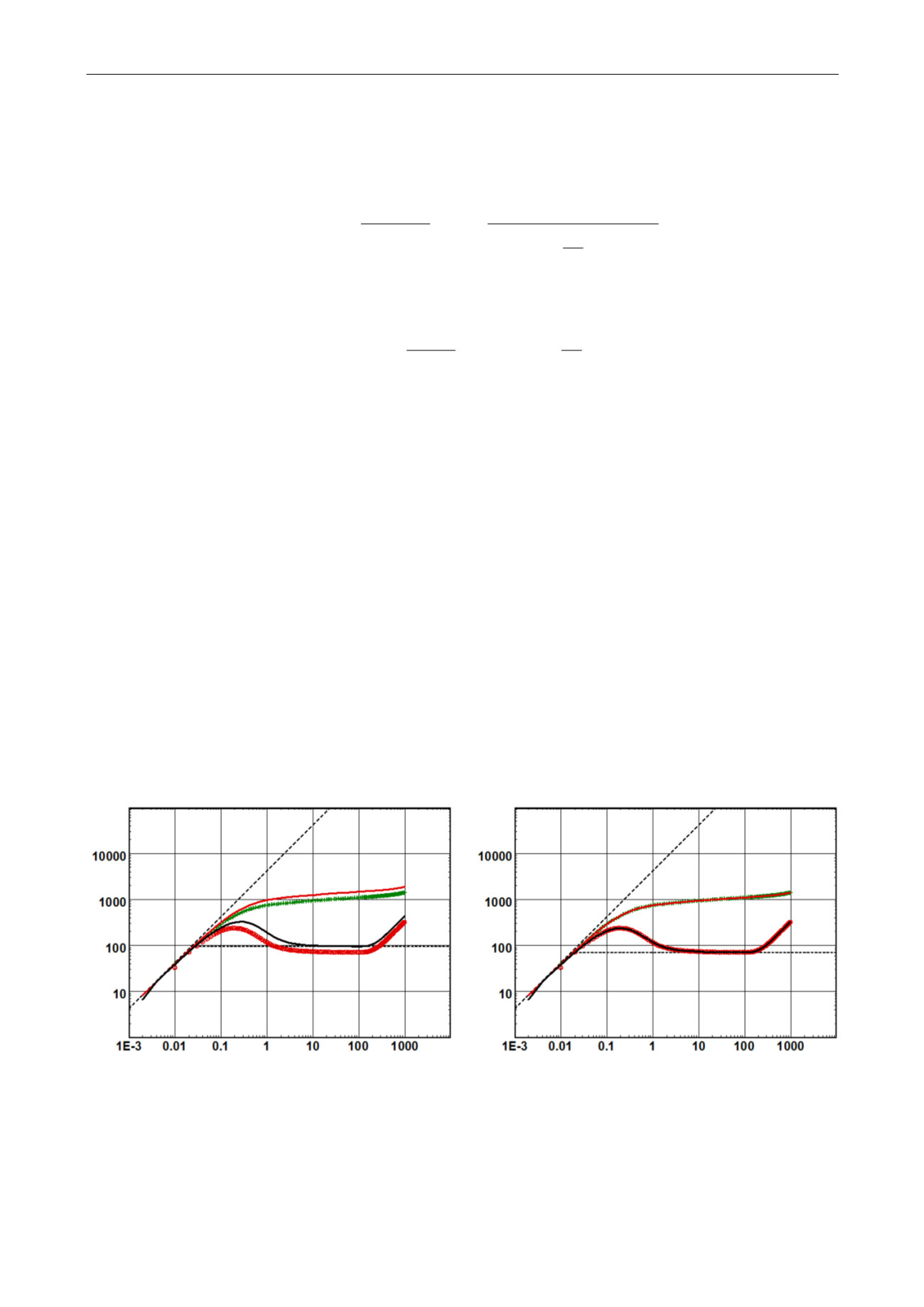
Fig. 2.H.23 – h at 25% below ‘true’ – Left plot is the model using all other ‘exact’ unknown
Right plot is the match after optimization of the unknown parameters
kh is OK – k is 33% above ‘true’ – re is 15% above ‘true’ – Skin at -0.14 instead of 0
















