
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 2 – T heory- p53/743
And the diffusion equation becomes:
x
p
Z
p
x
k
t
p
Z
p
c
x
t
0002637
.0
Or:
x
p
Z
p
x c
k
t
p
Z
p
t
x
0002637
.0
We add the viscosity
on both sides of the equation:
Gas diffusion equation:
x
p
Z
p
x c
k
t
p
Z
p
t
x
0002637
.0
2.I.3
Diffusion of real dry gas
2.I.3.a
Standard pseudopressures
In order to extend the methodology of Dynamic Data Analysis to gas cases, one introduces a
function of the pressure called the pseudopressure. It is given by:
Gas pseudopressure:
dp
Z
p
pm
p
0
2
The Derivation leading to this equation is detailed in the ‘chapter 13 - Analytical models - 13.E
- The use of pseudofunctions’.
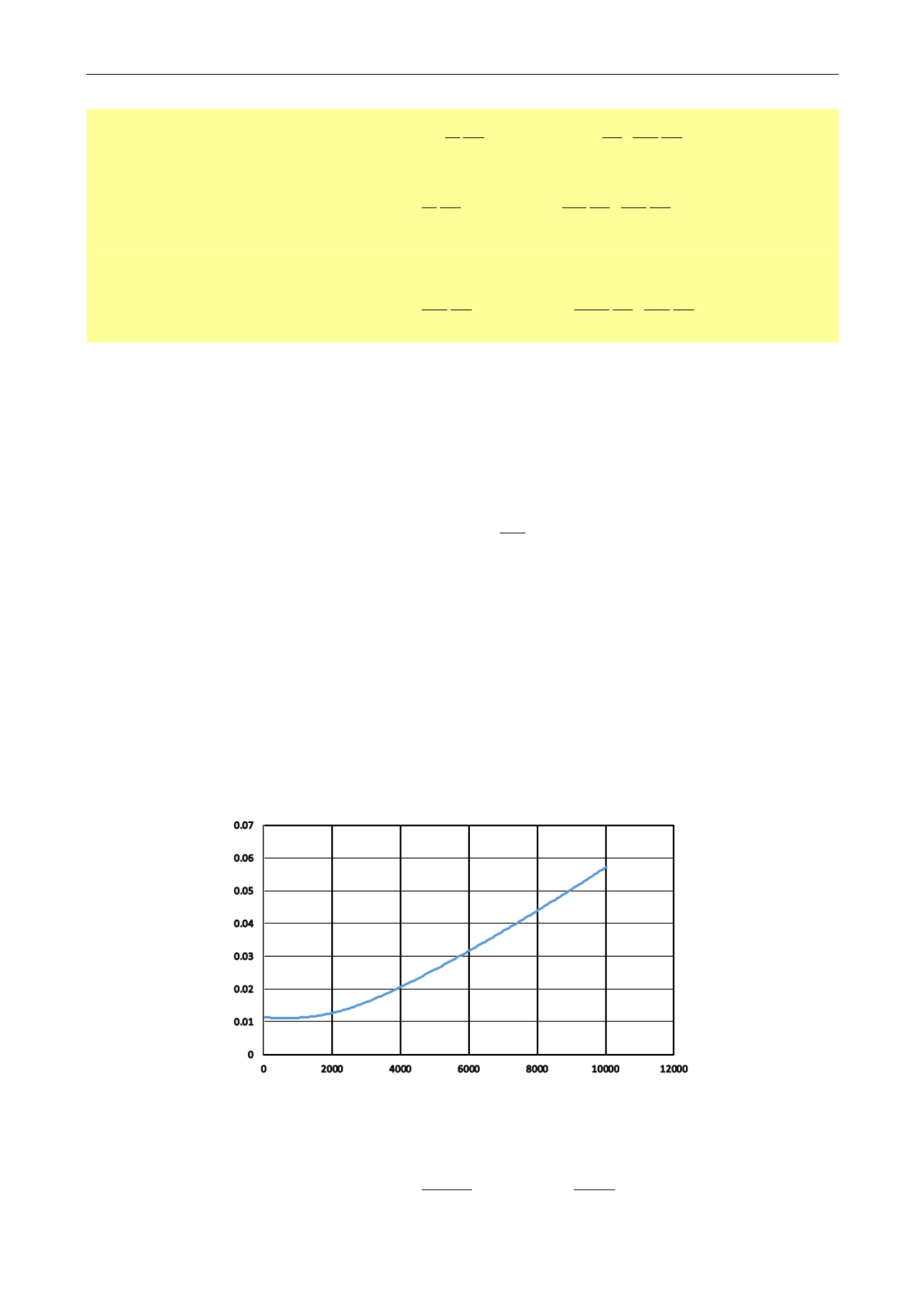
The Field unit for pseudopressures is psi²/cp. A typical the product
z
response as a function
of pressure, and for a given temperature, is shown below. There is a rule of thumb regarding
the behavior of this function:
Below 2000 psia,
Z is fairly constant, and m(p) behaves like p
2
Above 3000 psia,
Z is fairly linear, and m(p) behaves like p
Fig. 2.I.5 –
z vs p [psia)
Gas diffusion equation:
) (
0002637
.0
) (
2
pm
c
k
t
pm
t
















