
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 6 – W ell models -p184/743
6.D.6
Adding wellbore storage
The original publications on fracture solutions were without wellbore storage and skin. It is not
that it was absent, but the solution with two additional parameters (C and S) was too complex
to be turned into readable type-curves especially as the influence of skin is particularly messy.
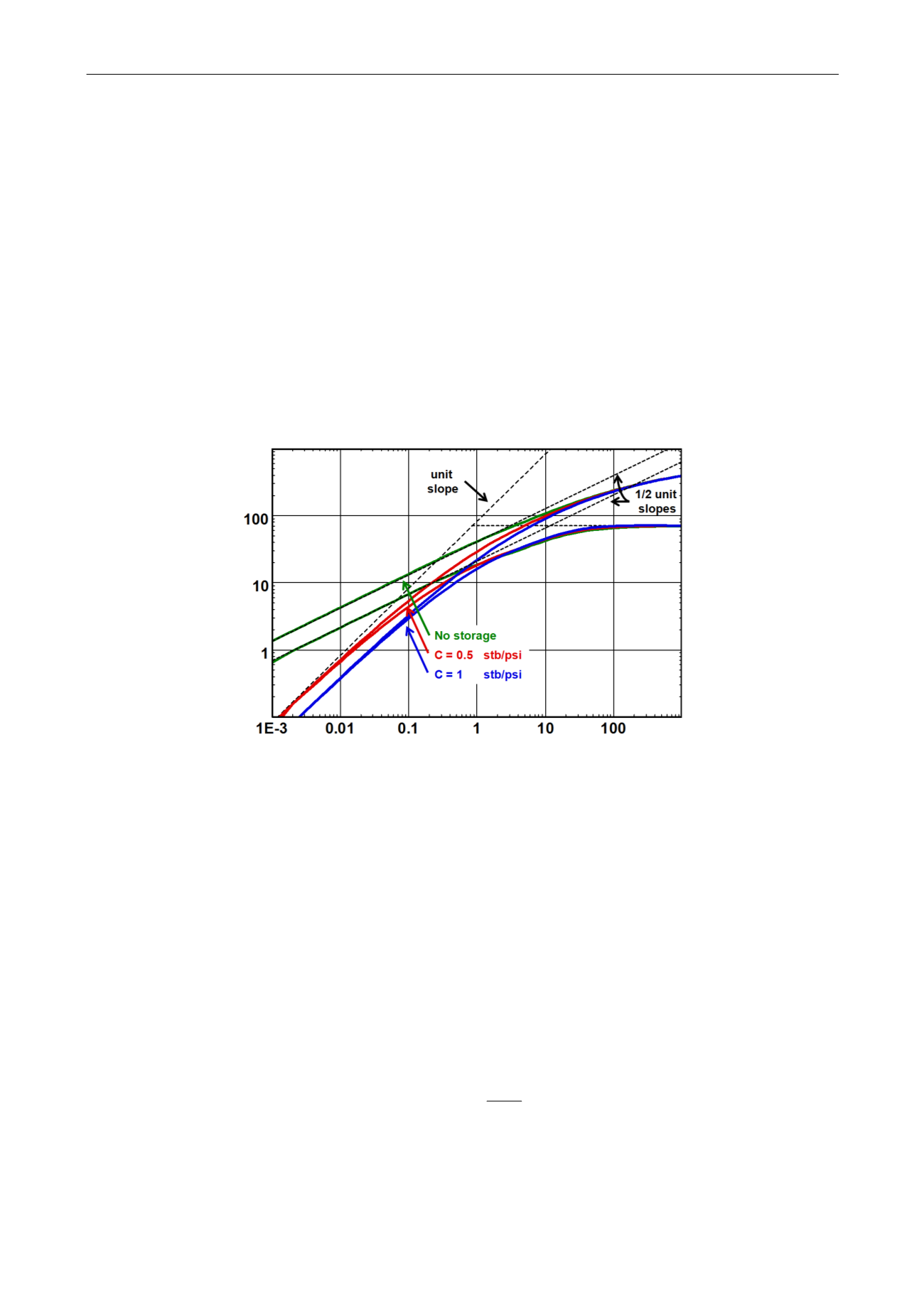
Wellbore storage will affect the early time data by masking the linear flow. If the storage effect
is high enough no fracture flow may be diagnosed from the loglog plot and the interpreter can
no longer justify that a fracture may exist if the total skin is not highly negative. It will also
become increasingly more difficult to make a choice between a low or high conductivity
fracture, and the half fracture length
X
f
can no longer be determined from the square root plot.
If a fracture job had been done on the well this could be an indication that the job had not
been very successful or that the fracture had propagated up or down rather than laterally.
The below figure illustrates the effect of wellbore storage on the linear flow in the loglog plot.
Fig. 6.D.10 – Loglog plot influence of wellbore storage
6.D.7
Skin effect
Total skin; geometrical skin; model skin: The concept of skin in configurations that are not
based on a standard vertical well are sometimes confusing. This section describes the different
skin components, and how they may be combined.
6.D.7.a
Fracture Geometrical Skin
When we run a standard straight line analysis on a logarithmic scale (MDH, Horner,
Superposition) we calculate a value of the skin factor. This is what we call the
Total Skin
S
T
.
This calculation may take place at any time after the extraction of the build-up, and is
independent of the model chosen. The Total Skin is given by the equation:
T
sf
Skin
S
kh
q
p
2. 141
where
p
Skin
is the pressure difference between our data and the response of a standard,
undamaged, fully penetrating vertical well.
















