
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 6 – W ell models -p181/743
6.D.4
Sensitivity to different parameters
6.D.4.a
Choice of fracture model
The description above applies to both Infinite Conductivity and Uniform Flux models. It may be
interesting at this stage to compare both solutions for the same parameters, see figure below.
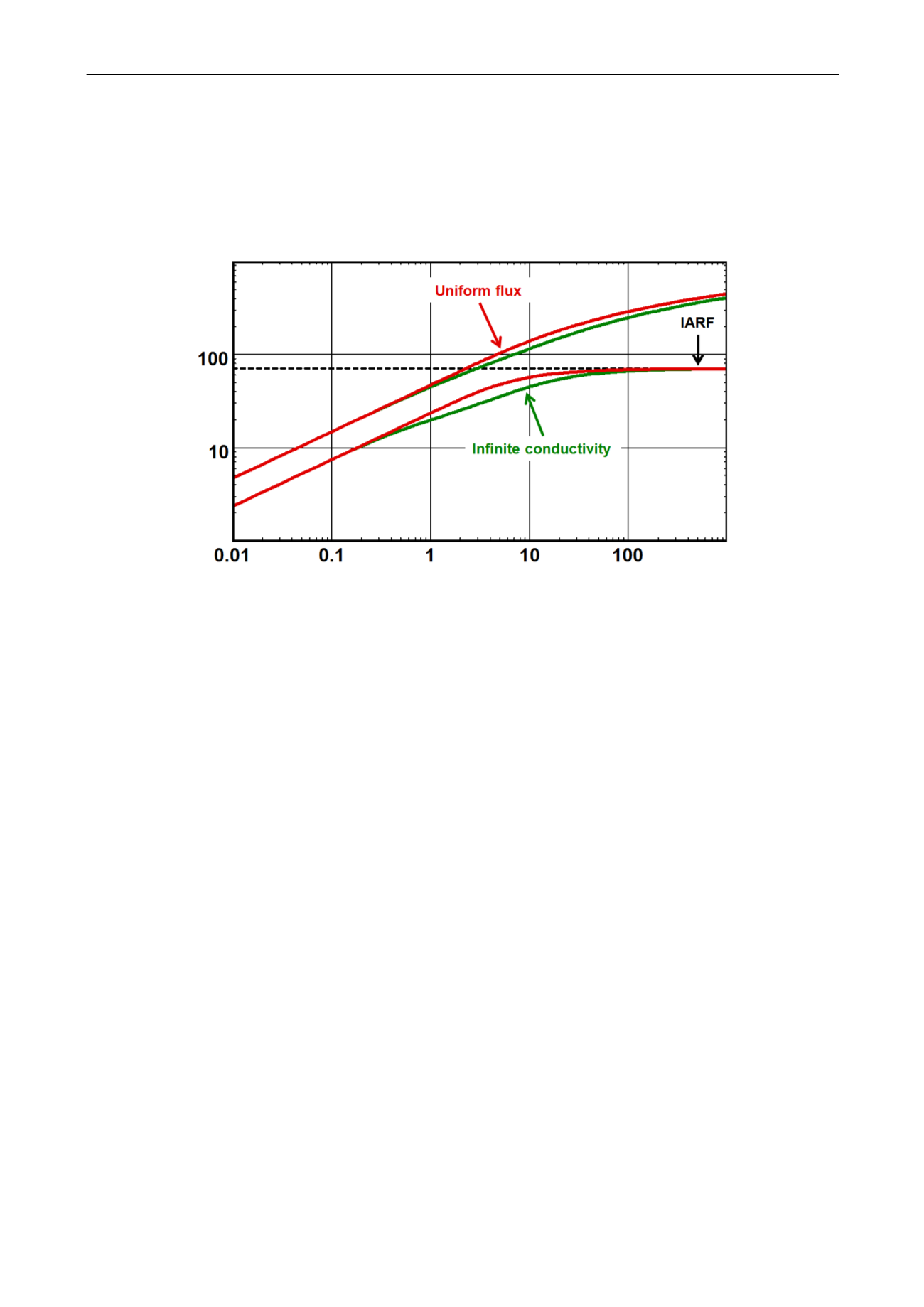
Fig. 6.D.6 – Uniform Flux vs. Infinite Conductivity
These solutions differ only slightly when plotted on a loglog scale. Purists consider that the
uniform flux solution is physically incorrect and only the infinite conductivity solutions should
be used. In real life the uniform flux transients generally offer a better match, and this can be
explained by the fact that the productivity of the uniform flux fracture, for a given length, is
slightly lower than the infinite conductivity, and that this, possibly, better simulates the slight
pressure losses in the fracture.
The Uniform Flux model was published because it was fairly easy to calculate. The infinite
conductivity fracture was solved semi-analytically (at high CPU cost) but it was shown that an
equivalent response could be obtained by calculating the (fast) uniform flux solution at an off-
centered point in the fracture (x=0.732.X
f
). This position corresponds to the intercept of both
flow profiles, as shown in the ‘behavior’ section.
6.D.4.b
Sensitivity to the half fracture length
The loglog plot below is the comparison of several infinite conductivity responses for different
values of X
f
, all other parameters, including the formation permeability, staying the same.
Because the permeability does not change, the pressure match remains constant, and the
loglog response is shifted left and right. Multiplying the fracture length by 10 will shift the
responses two log cycles to the right. This will shift the early time half slope down one cycle.
















