
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 6 – W ell models -p183/743
6.D.5
Specialized Analysis
Let us repeat it. The loglog analysis with the Bourdet derivative (a.k.a. the ‘right stuff’) has all
what is needed to perform the complete analysis of a fractured well. Positioning the half slopes
of both pressure and Bourdet derivative exactly does what we will be showing below. The
advantage of the loglog approach is that it will be valid even if a pure linear flow is not
detected, and a successful nonlinear regression will not require pure behaviors to occur.
Anyway, the specialized analyses have a historical value and do not hurt, anyway.
From the previous section, the relation between pressure and time during the linear flow is:
2
2
2 2
1
52.16
f
t
kX
ch
Bq
m where
t mp
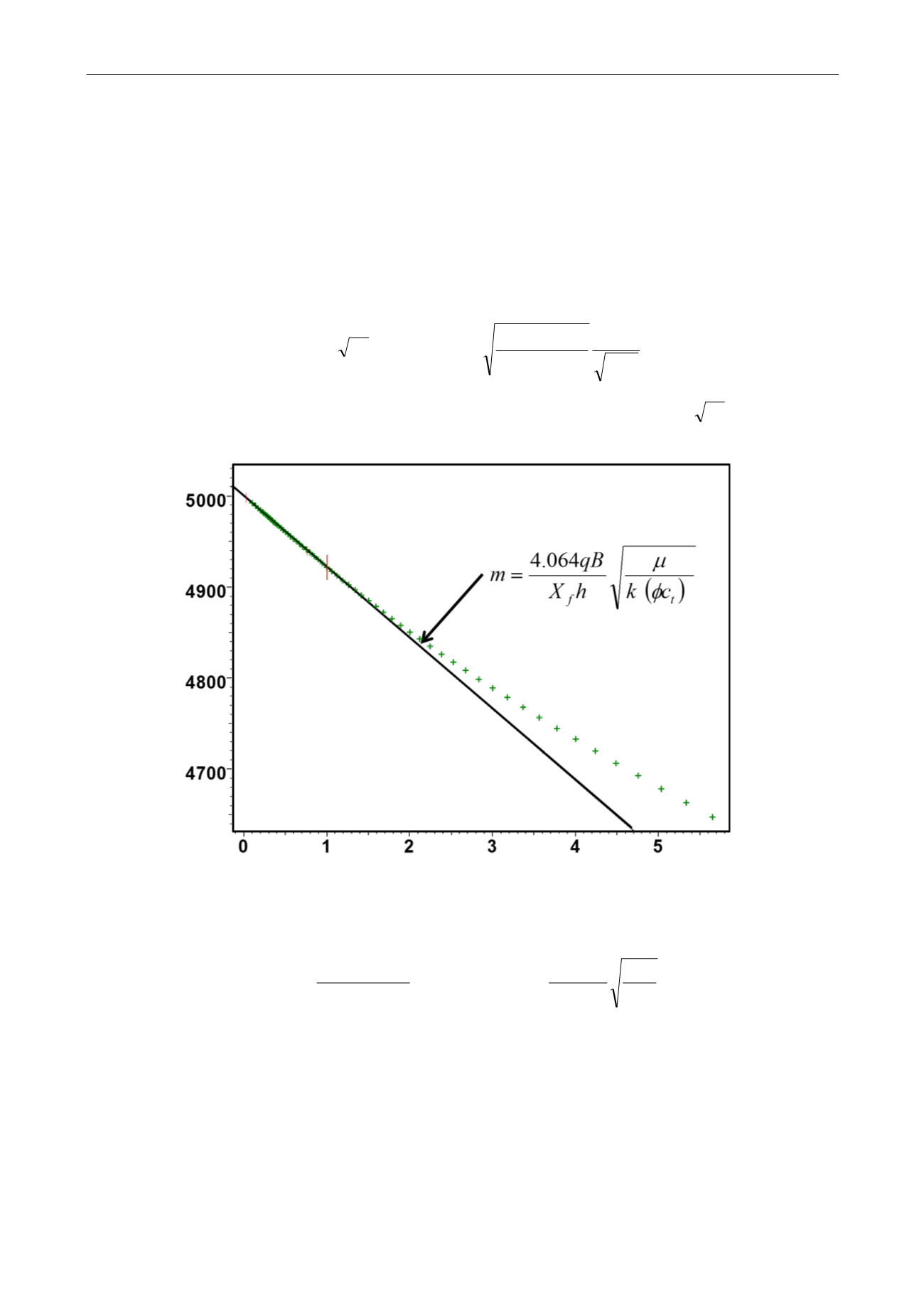
A straight line can be drawn on a cartesian graph of pressure change versus
t
:
Fig. 6.D.9 – Square root plot
From this plot we get a value of
kX
f
²
, and therefore
X
f
if we do know
k
.
t
f
t
f
ck
mh
qB
X or
and
chm
Bq
kX
06.4
/
52.16
22
2 2
2
Applying superposition?
NO!
In a specialized plot (except the linear plot) it is possible to replace a time function by its rate
superposition. For example we could use the tandem square root plot in the case of a build-up.
This is the case when we assume that the flow regime we are studying is actually the
superposition of these flow regimes. We do this for Infinite Acting Radial Flow or late time
effects such as the linear flow between parallel faults. This does NOT apply here, or to any
other early time behavior, and we should use the pure time function, not the superposed one.
The only exception may be for shale gas, where the ‘early time’ behavior actually lasts years,
and where superposition may be applicable.
















