
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 6 – W ell models -p180/743
6.D.3
Loglog Analysis
From the previous section, the pressure change during the early time linear flow is:
2
2
2 2
1
52.16
f
t
kX
ch
Bq
m where
t mp
In the equations above, all parameters are inputs except the permeability and the fracture half
length. During the linear flow, the result of any analysis will therefore provide a relation
between permeability and fracture half length by determining the value of kX
f
².
The Bourdet derivative at early time is given by:
p t m
t
m
t
td
pd
t
t
d
pd
p
2
1
2
1
2
)
ln(
'
On a decimal logarithmic scale this writes:
)2 log(
)
log(
)'
log(
)
log(
2
1
)
log(
)
log(
p
p
and t
m p
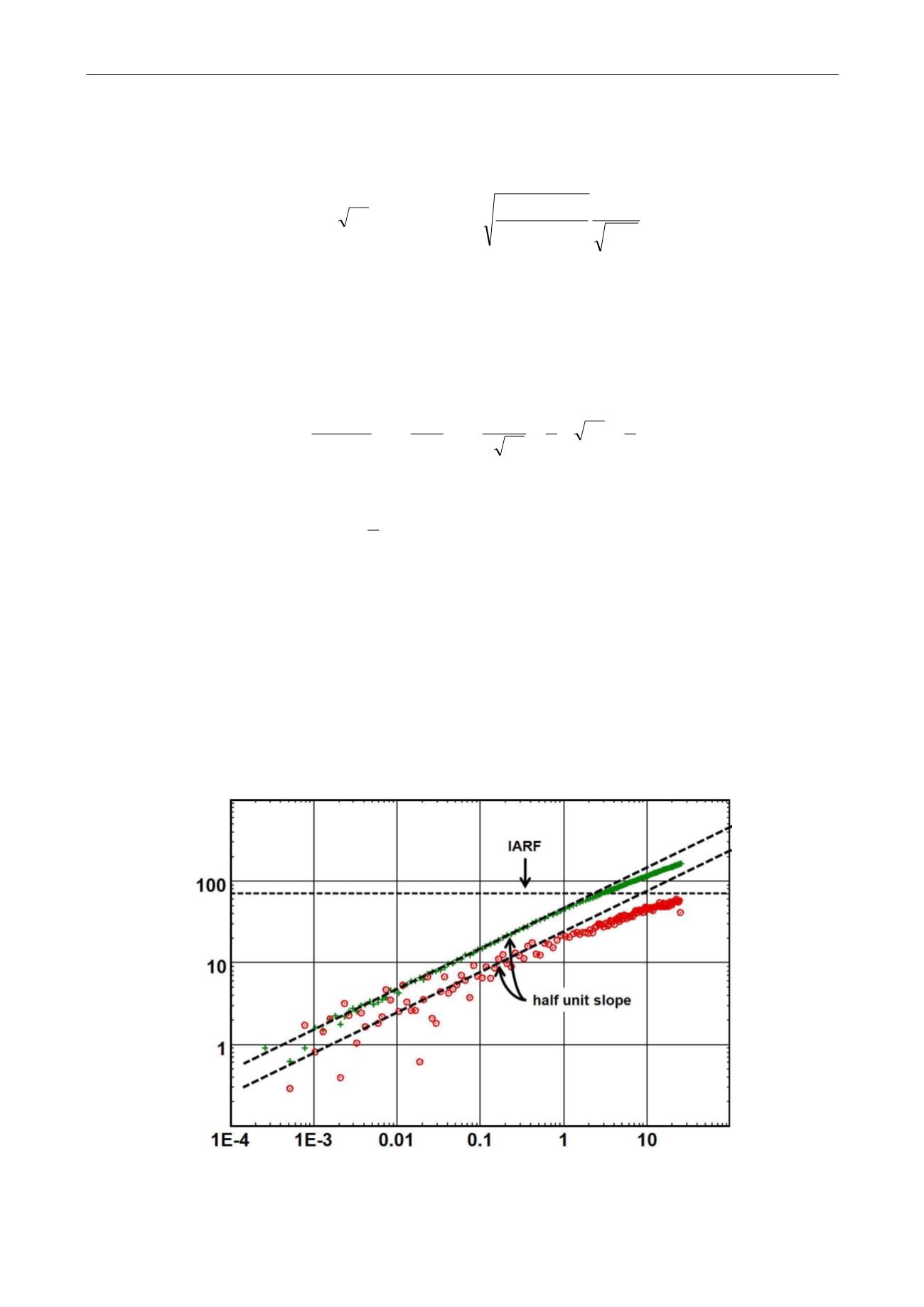
The early time flow regime of a high conductivity fracture is characterized on a loglog plot by a
half unit slope on both the pressure and derivative curves. The level of the derivative is half
that of the pressure. At later time there is a transition away from this linear flow towards
Infinite Acting Radial Flow, where derivative stabilizes (see figure below).
The position of these two half slope straight lines will establish a link between the time match
and the pressure match, providing a unique result for
kX
f
²
. Fixing the stabilization level of the
derivative will determine the value of
k
, and the half fracture length will be calculated from
kX
f
²
. If there is no clear stabilization level the problem will become underspecified.
Fig. 6.D.5 – Infinite conductivity fracture behavior
















