
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 6 – W ell models -p187/743
6.E
Low conductivity fracture
6.E.1
Hypothesis
The fracture geometry is the same as that of the high-conductivity models, but now it is
assumed that there is a significant pressure gradient along the fracture.
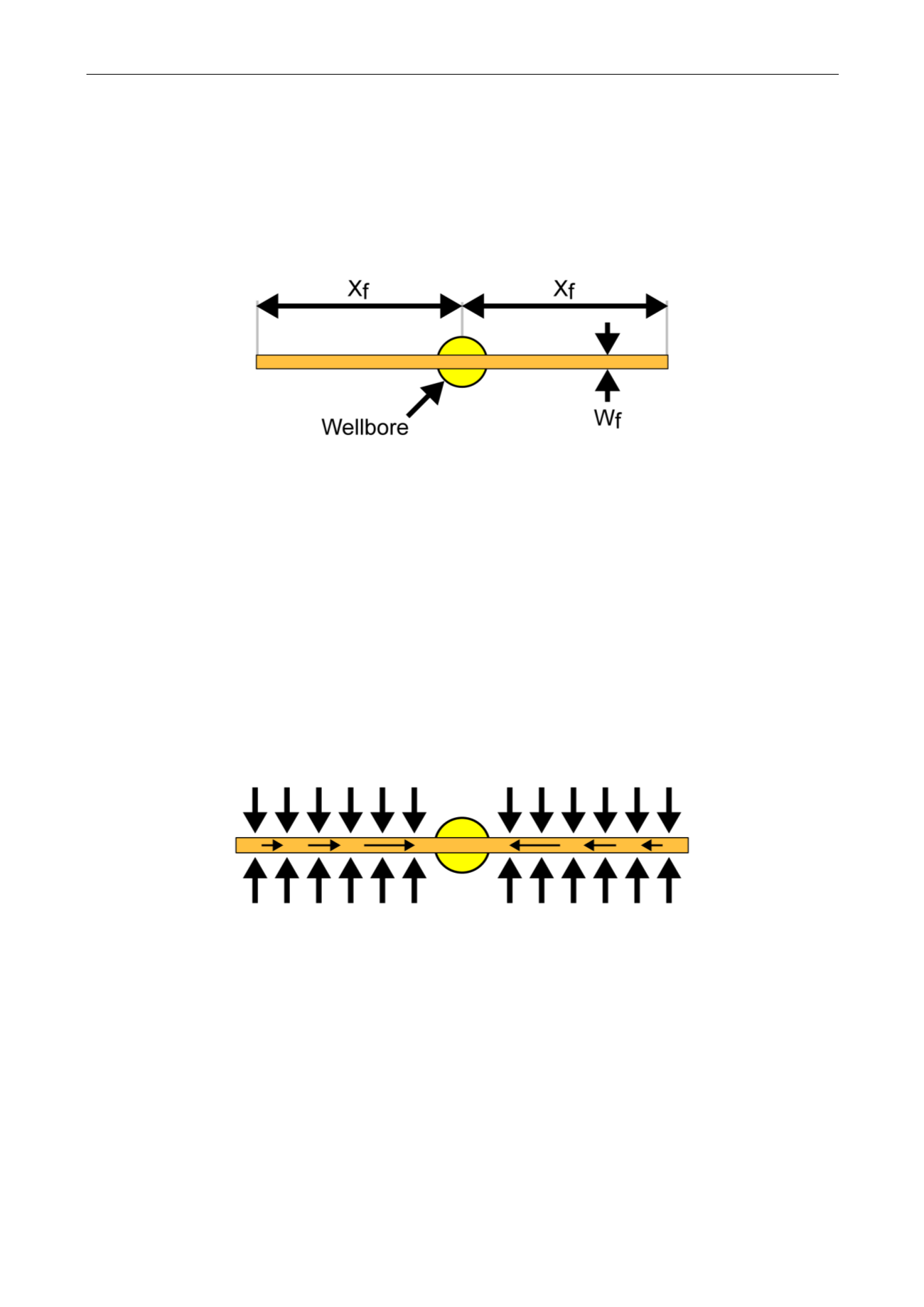
Fig. 6.E.1 – Schematic of a fracture model in the horizontal plane
6.E.2
Behavior
In the absence of storage, the first flow regime is linear flow along the fracture axis, this
simultaneously induces a linear flow orthogonal to the fracture, the amplitude of which
changes along the fracture length, i.e. there is a non-uniform flux into the fracture, in contrast
to the high-conductivity models. This bi-linear flow regime, with linear flow along two axes,
gives rise to a pressure response proportional to the fourth root of time. Both the loglog and
the Bourdet derivative plots exhibit quarter slopes during bi-linear flow. Bi-linear flow is
followed by the usual linear flow, characterized by a 1/2-unit slope on the loglog.
Fig. 6.E.2 – Early time bi-linear flow
The bi-linear flow regime is usually happening at very early time, and is not always seen. It
represents the time at which the pressure drop along the fracture is significant, and in reality
this time is very short. Even when there is no storage effect, the data sometimes does not
exhibit a ¼-slope and can be matched directly with a high-conductivity fracture model.
However, the general model for an ‘induced fracture’ fractured well must be the finite-
conductivity fracture model, as there will always be a pressure drop along the fracture,
however small. This is however, not significant compared to the linear pressure drop in the
reservoir into the fracture.
















