
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 4 – R ate Transient Analysis (RTA)- p139/743
So the linear relationship between dimensionless rate and cumulative becomes:
w i
t
i
p p Nc
QB
pw pkh
qB
615 .5
8936 .0
2
1
2. 141
Using the full definition of the dimensionless variables requires an a priori estimate of PV,
basically what we are after. Therefore the method presented by Agarwal-Gardner is iterative.
However we see from the above equation that if we plot
w i
p p
q
versus
w i
t
p pc
Q
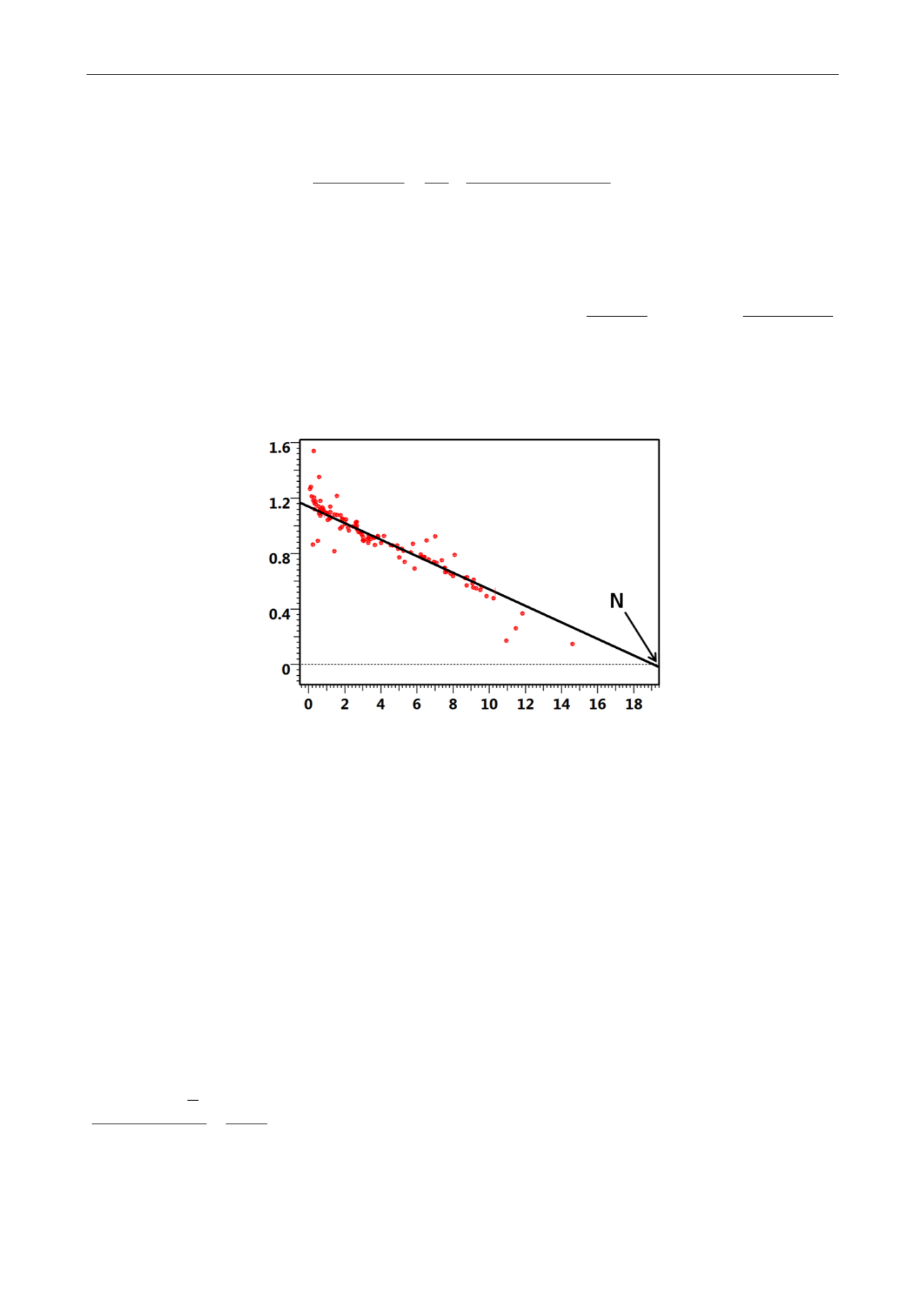
boundary dominated flow will exhibit a straight line which intercept with the X axis gives
directly N.
Fig. 4.C.8 – Material balance plot
Note: In the case of constant flowing pressure, it is interesting to draw a parallel between this
rate cumulative plot and the rate cumulative plot used in traditional decline curve analysis. The
traditional decline methods yield a maximum recovery rather than fluid in place. The relation
between the two methods is established by considering a recovery factor of RF=
w i
t
p pc
.
4.C.4
Flowing gas material balance plot
The principle is to get from flowing data a plot that resembles a normal P/Z plot made in terms
of reservoir average pressure. As always the problem with this kind of analysis is that one
needs the results sought to build the plot, leading to an iterative procedure.
The Material Balance equation in gas is written:
b t
Gc
q
pm pm
a
i
i
t
t
n
i
n
1 )(
) (
)(
(1)
















