
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 4 – R ate Transient Analysis (RTA)- p138/743
4.C.3
Material balance (Normalized rate-cumulative) plot
Agarwal
et al.
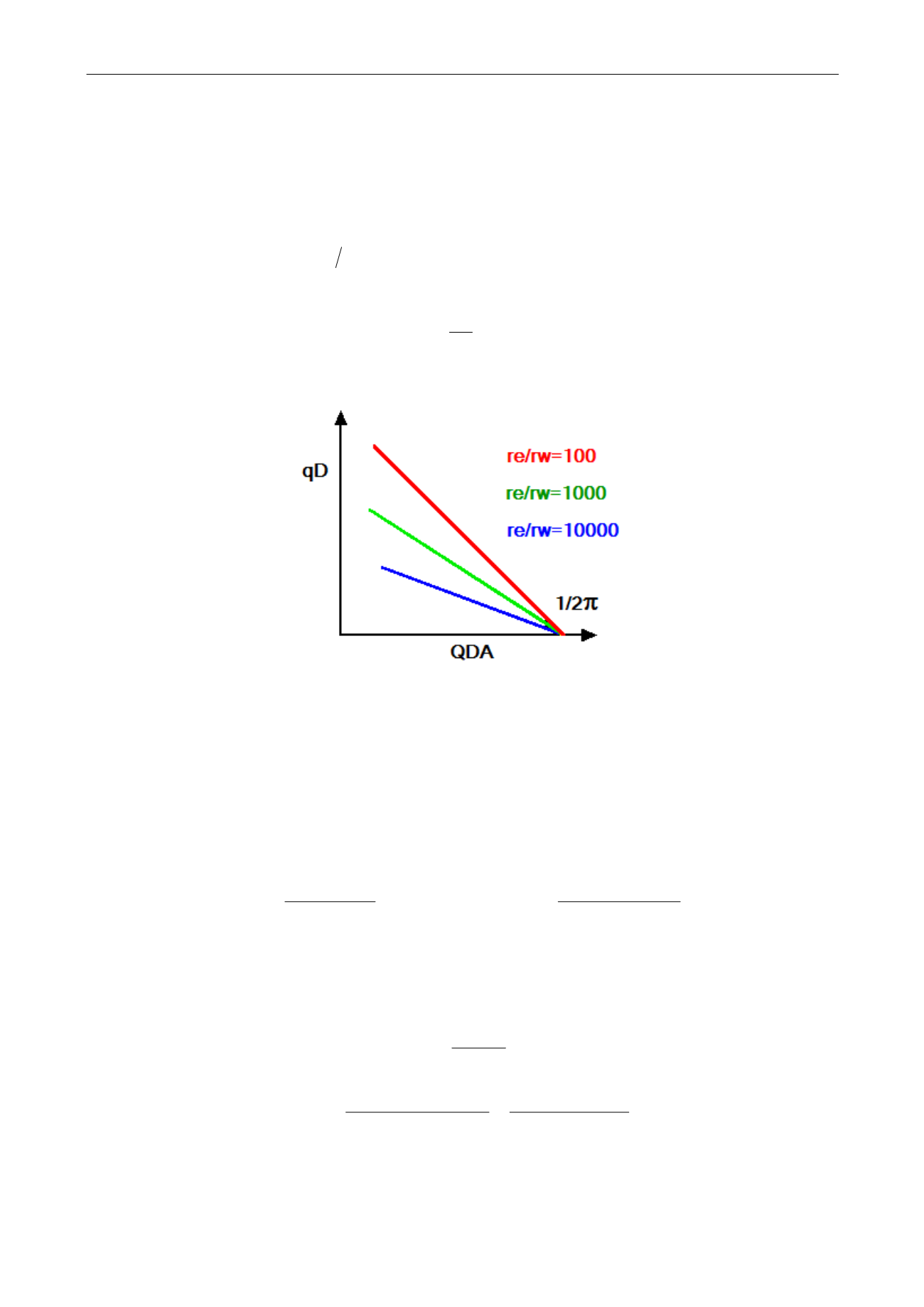
presented a Cartesian plot of dimensionless rate q
D
versus dimensionless
cumulative Q
DA.
They show that the responses corresponding to distinct reservoir sizes all exhibit a straight line
with a negative slope during boundary dominated flow, and all curves converge to the same
value on the X axis, equal to
21
. In other words, the following relation is established in all
cases during boundary dominated flow:
DA
D
Q
q
2
1
Fig. 4.C.7 – Agarwal et al plot
The expression of the dimensionless variables varies depending of the fluid type and a specific
treatment must be applied in each case.
Oil
For an oil case, the expression of the dimensionless parameters is defined below:
pw pkh
qB
q
i
D
2. 141
and
w i
t
DA
p p hAc
QB
Q
8936 .0
All equations are in Oil Field units.
The dimensionless cumulative production can be expressed in terms of the fluid in place, in
STB/D:
B
hA
N
615 .5
w i
t
w i
t
DA
p p Nc
Q
p p Nc
Q
Q
2
615 .5
8936 .0
















