
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 4 – R ate Transient Analysis (RTA)- p136/743
4.C.2
Loglog plot
By replacing the time with an equivalent time, defined as the ratio of the cumulative to the
flow rate, one can transform a variable flowing pressure test into a constant rate equivalent, at
least for a liquid case. The parallel with constant rate solution can be taken one step further if,
rather than working with a pressure-normalized rate, we work with rate-normalized pressure.
In other words for the liquid case, if we plot
p p t
q t
i
w
versus
t
Q t
q t
e
on a loglog scale the
boundary dominated flow will exhibit a unit slope line, similar to pseudo-steady state in
Pressure Transient Analysis. Furthermore, if we take the derivative of the normalized pressure
with respect to the logarithm of
t
e
, the transient part will exhibit a stabilization at a level
linked to the mobility.
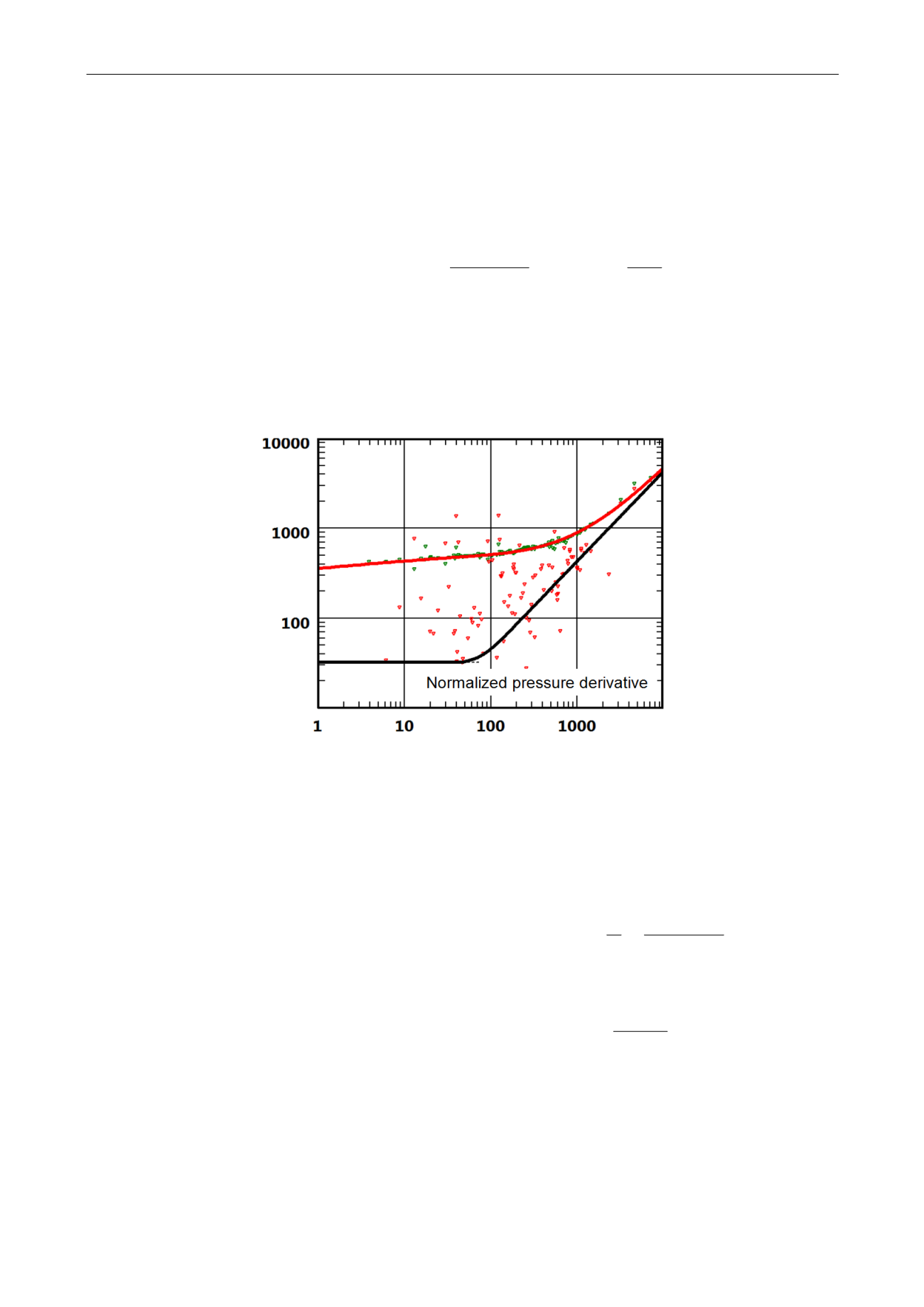
Fig. 4.C.4 – Loglog plot with normalized pressure derivative
The similarity with PTA is thus complete. Yet, the noise level on the derivative is usually too
high, see the figure above. One workaround is to work with a normalized pressure integral, in
a manner analogous to what was done on the Palacio-Blasingame type-curves.
Integral of normalized pressure:
d
q
p p
t
tI
e
t
o
w i
e
e
1
Bourdet derivative of the Integral of normalized pressure:
e
e
e
t
tI
t I
ln
'
















