
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 2 – T heory- p20/743
2.C
Line Source Solution in a homogeneous infinite reservoir
We now consider the simplest problem we can find: the diffusion in a homogeneous infinite
reservoir, starting at initial uniform pressure p
i
, produced by a vertical line source well. The
introduction to dimensionless terms and the derivations for this model are shown in the
Chapter ‘Analytical models - 13.B - Dimensionless problems’.
2.C.1
The Line Source Solution
The solution in dimensionless terms is given in the paragraph ‘13.B - Dimensionless problems’.
To get the physical solution, the dimensionless parameters are replaced by their real values.
The solution at any point and time, for a Line Source well producing a homogeneous infinite
reservoir, is then given by the following:
Line Source Solution:
kt
rc
E
kh
qB
p trp
t
i
i
2
1. 948
6.70
,
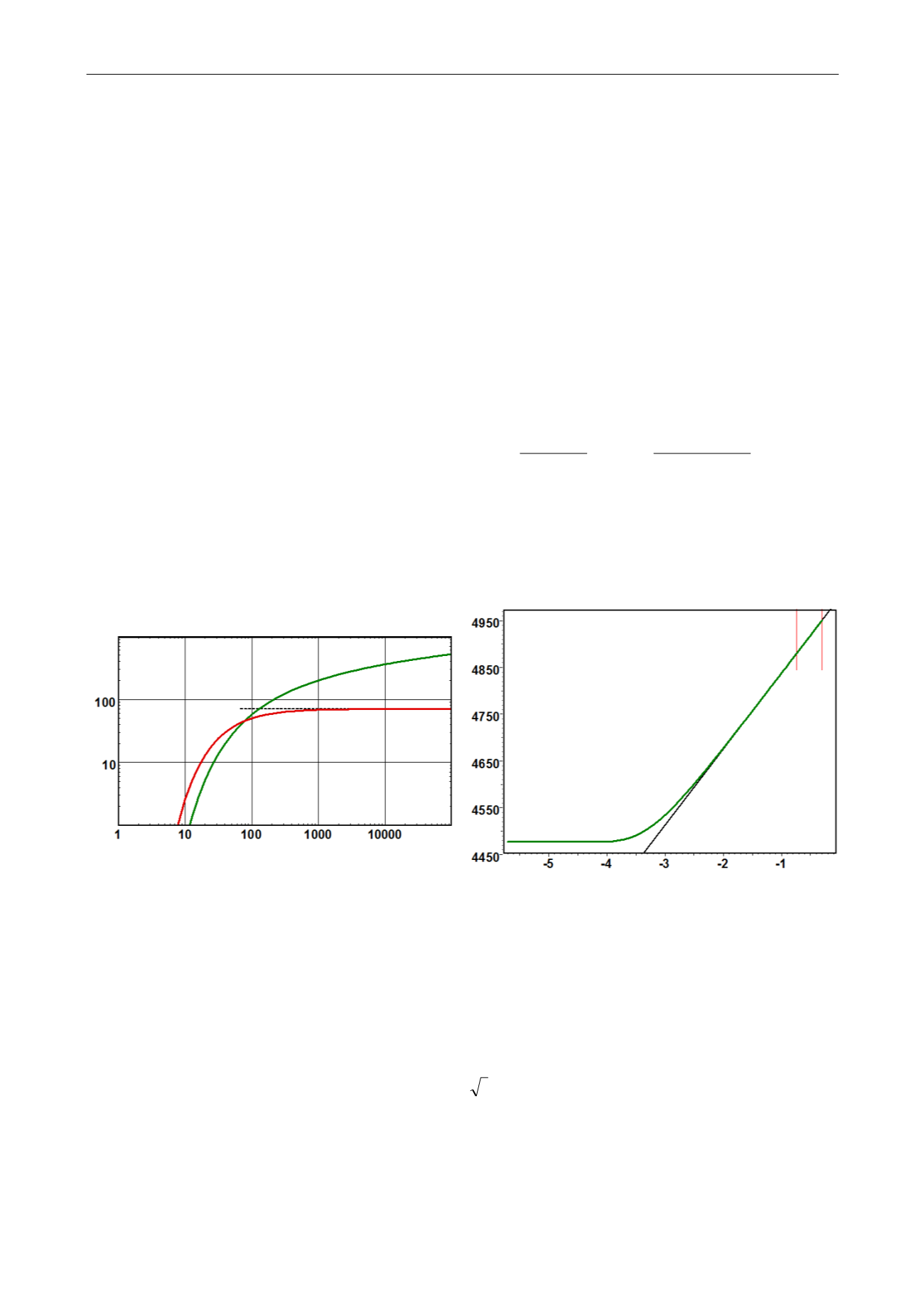
A typical line source response is displayed in the figures below, on a loglog scale (with the
Bourdet derivative) and a semilog scale. For first readers, the notions of loglog and semilog
plots are described in the PTA methodology chapter.
Fig. 2.C.1 – Line source loglog plot
Fig. 2.C.2 – Line source semilog plot
The line source equation shows that the pressure change is a unique function of the parameter
group r
2
/t, or more conveniently r/√t. This has an important implication on the physical
understanding of the diffusion process. If one considers, for example, the time it requires for
the pressure change to reach a certain value (for example 1 psi), it will amount to a certain
value of r/√t that we will calculate from the Line Source Solution, and therefore the relation:
Radius of investigation:
ta r
inv
In the chapter on boundary models we recommend at one does not use the notion of radius of
investigation, as it may be misleading when one considers how such result is used afterwards.
However, it is an interesting means of understanding the diffusion process. To extend this
notion to cases where the flow geometry may not be strictly radial, we may consider that the
area of investigation is proportional to r², and we therefore have:
















