
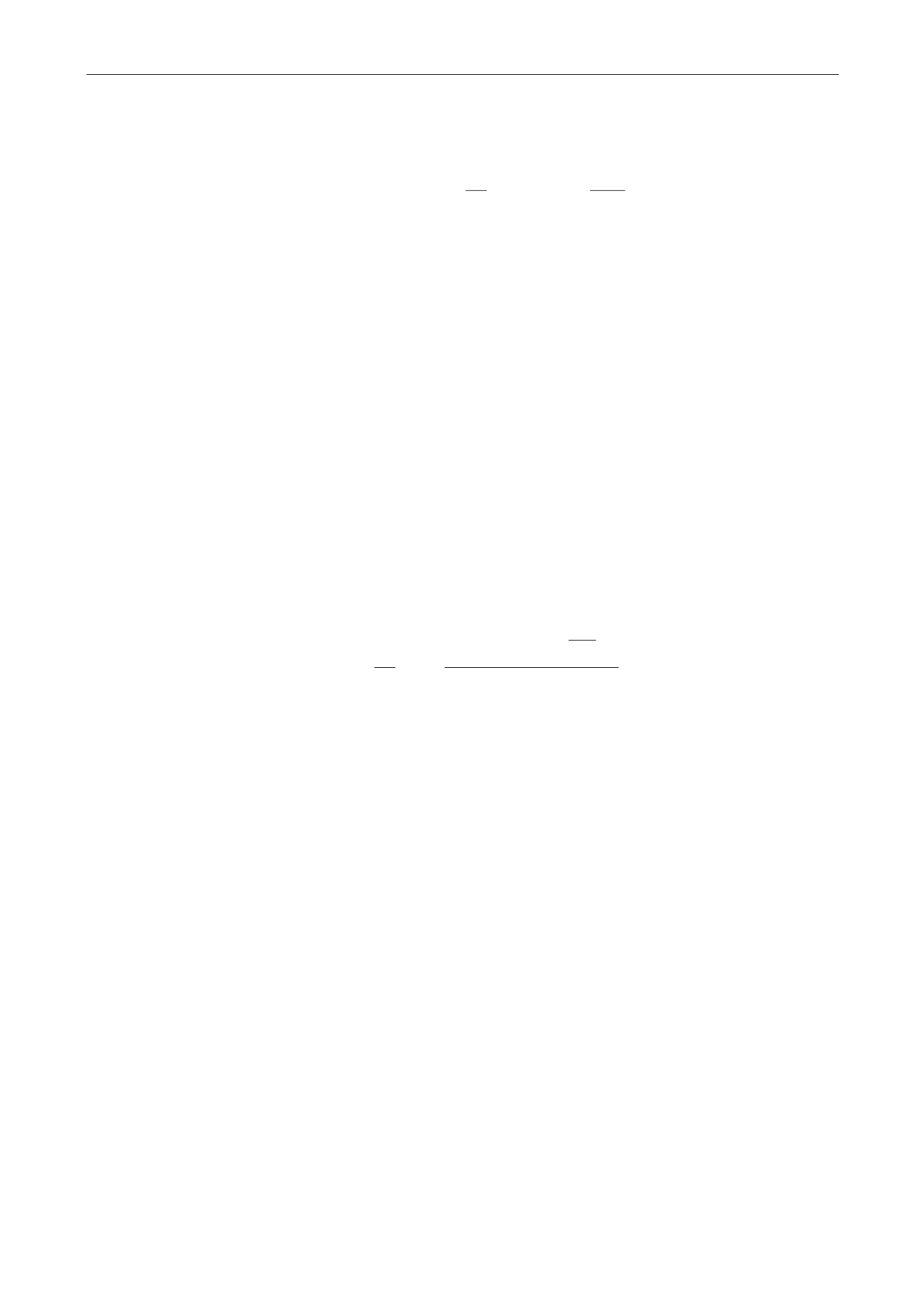
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 2 – T heory- p19/743
An unrealistic but very convenient model of well condition is the line source, corresponding to
the same Darcy’s law but for the limit case of a well of radius zero.
Line source well:
kh
qB
r
p
r
t
r
2. 141
lim
,0
The line source problem is interesting because it is easier to solve, faster to run and the
calculation of this solution at r=r
w
is a good approximation of the finite radius solution and for
any practical purpose it is exactly the same solution within the formation, when r>r
w
. It is the
solution of choice to simulate interference tests and image wells for boundary effects (see the
chapter on boundary models).
Other inner boundary conditions correspond to Darcy’s law applied to more complex well
geometries (fractures, limited entry, horizontal, slanted, multilateral, etc), and are detailed in
the chapter on well models.
In most cases, the production of the well will be affected by wellbore effects, generally
modelled using what we call the wellbore storage. This notion is developed in the Wellbore
chapter.
In these cases there is a time delay in the production / shut-in, and the well condition also
includes a wellbore component. The simplest model is a constant wellbore storage applied to a
well opened and shut in at surface. The modified equation, for a finite radius well, with
wellbore storage:
kh
t
p
C qB
r
p
r
t r
w
24
2. 141
,
2.B.3
Outer boundary conditions
Another set of equations is needed to define how the fluid reacts close to a natural boundary.
This could be the outer boundary of the system, or even intermediate faults.
The simplest condition to model analytically is that there is no boundary at all, i.e. that the
reservoir is of infinite extent in all directions. The equation for such system is:
Assuming radial symmetry:
i
r
p
trp
,
lim
Naturally and unfortunately, no reservoir is infinite. However, in pressure transient analysis
this model is easier to generate and will match the data over the duration of the well test, as
long as the test is short enough for no lateral boundary to be seen.
Infinite reservoir models are unlikely to be used in rate transient analysis, where such a
hypothesis is unlikely to be met over the extended time range of such analysis.
















