
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapter
3 – P ressure Transient Analysis (PTA)- p67/743
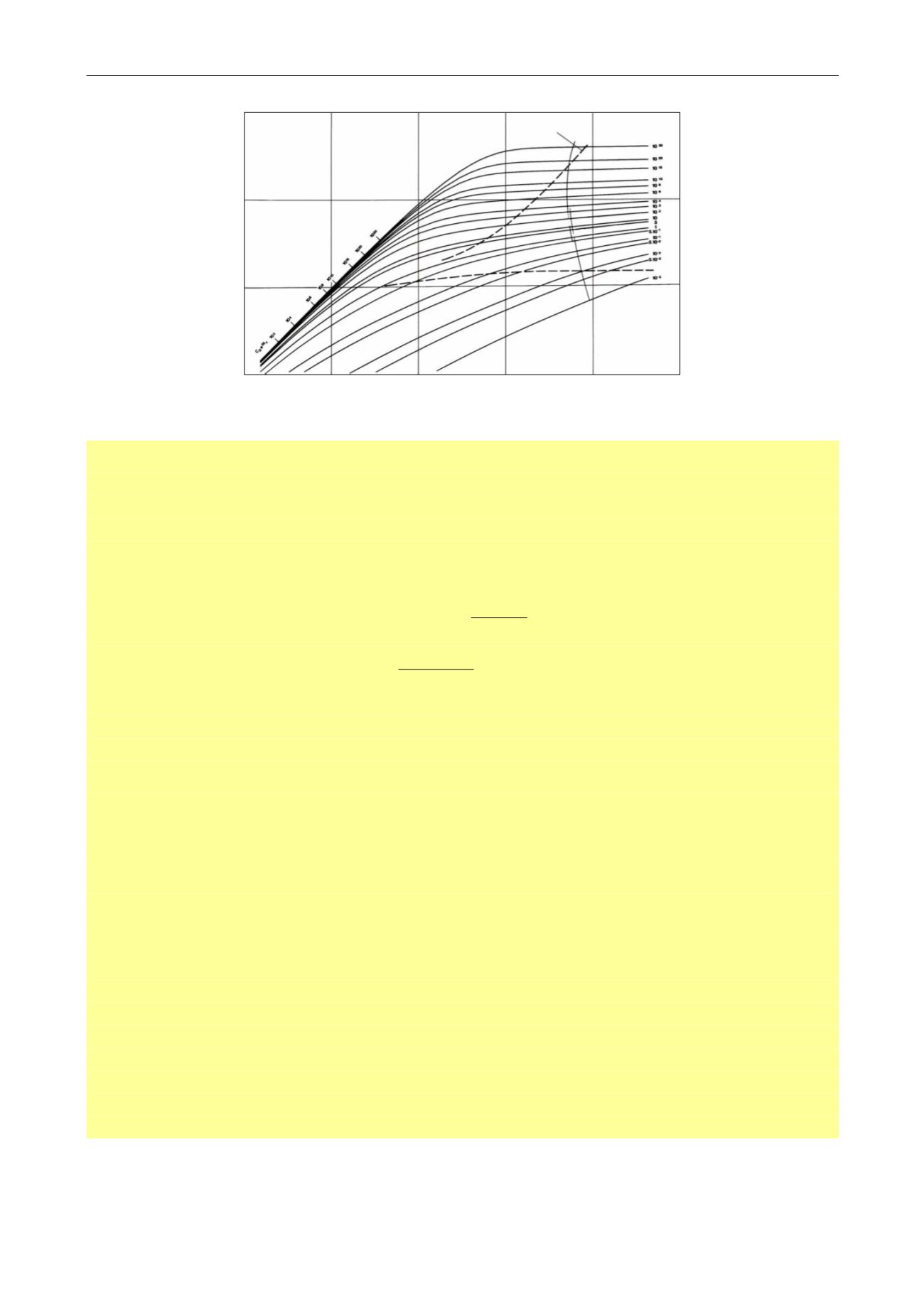
Fig. 3.B.6 – Wellbore storage and skin type-curve
The origin of type-curves
We have seen in Chapter ‘Theory’ that diffusion problems were solved by replacing the real
variables by dimensionless variables that eliminate other parameters influence in order to
arrive at a set of equations that are solved, hopefully quite simply and once and for all, in
dimensionless space. Two critical variables are the dimensionless time and dimensionless
pressure.
Dimensionless time:
tA t
rc
k
t
wt
D
2
0002637
.0
where
,...)
, ,(
w
r kf A
Dimensionless pressure:
pBp
qB
kh
p
D
2. 141
w
here
,...)
, ,(
hkgB
This is still used today in modern software to generate analytical models. The solution is solved
in dimensionless space, then the variables are converted to real variables and superposition is
applied to the solution, and then matched with the real data.
However, this was not possible, or at least not easy, before personal computers and related
software were available. So the ‘trick’ was to use a simple and remarkable property of the
logarithmic scales, historically used to create slide rules. Taking the logarithm of the equations
above we would get:
Logarithmic relations:
A t
t
D
log
log
log
and
B p
p
D
log
log
log
In other words, the dimensionless response, also called a type-curve, and the real response,
taken on a loglog scale, have the same shape. By translation, it is possible to match the data
on the dimensionless response and this is called a type-curve match. The value of the
translation, also called match point, in the X direction (the time match) and in the Y direction
(the pressure match) will give A and B, which in turn provides two quantitative pieces of
information. The time match will give different, model dependent, information. The pressure
match will typically give the permeability-thickness product.
















