
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 2 – T heory- p29/743
2.E.2
Derivation for a circular reservoir
We consider a finite radius well to which we will add later wellbore storage and skin. Because it
is an easy extension we are going to solve both cases of no-flow and constant pressure.
The problem is defined by the following set of equations:
Homogeneous radial diffusion:
r
p
r
r rc
k
t
p
t
1
0002637
.0
Finite radius well:
kh
q
r
p
r
sf
t r
w
2. 141
,
Uniform initial pressure:
i
p r tp
,0
Boundary equation, closed circle:
0
,
tr
e
r
p
Boundary equation, ct pressure circle:
i
e
p rtp
,
Dimensionless parameters are exactly the same as for the infinite finite radius solution and will
not be repeated here. We end up with the following dimensionless problem:
Homogeneous radial diffusion:
D
D
D
D D D
D
r
p
r
r r
t
p
1
Initial pressure & finite radius well:
0 ,0
D
DD
r
t p
1
,1
D D
t
r D
D
D
r
p
r
Closed circle OR Ct pressure circle:
0
,
t r D
D
eD
r
p
OR
0
,
eD DD
r t p
As for the line source problem we move the diffusion equation into Laplace space and get the
following generic solution using modified Bessel functions:
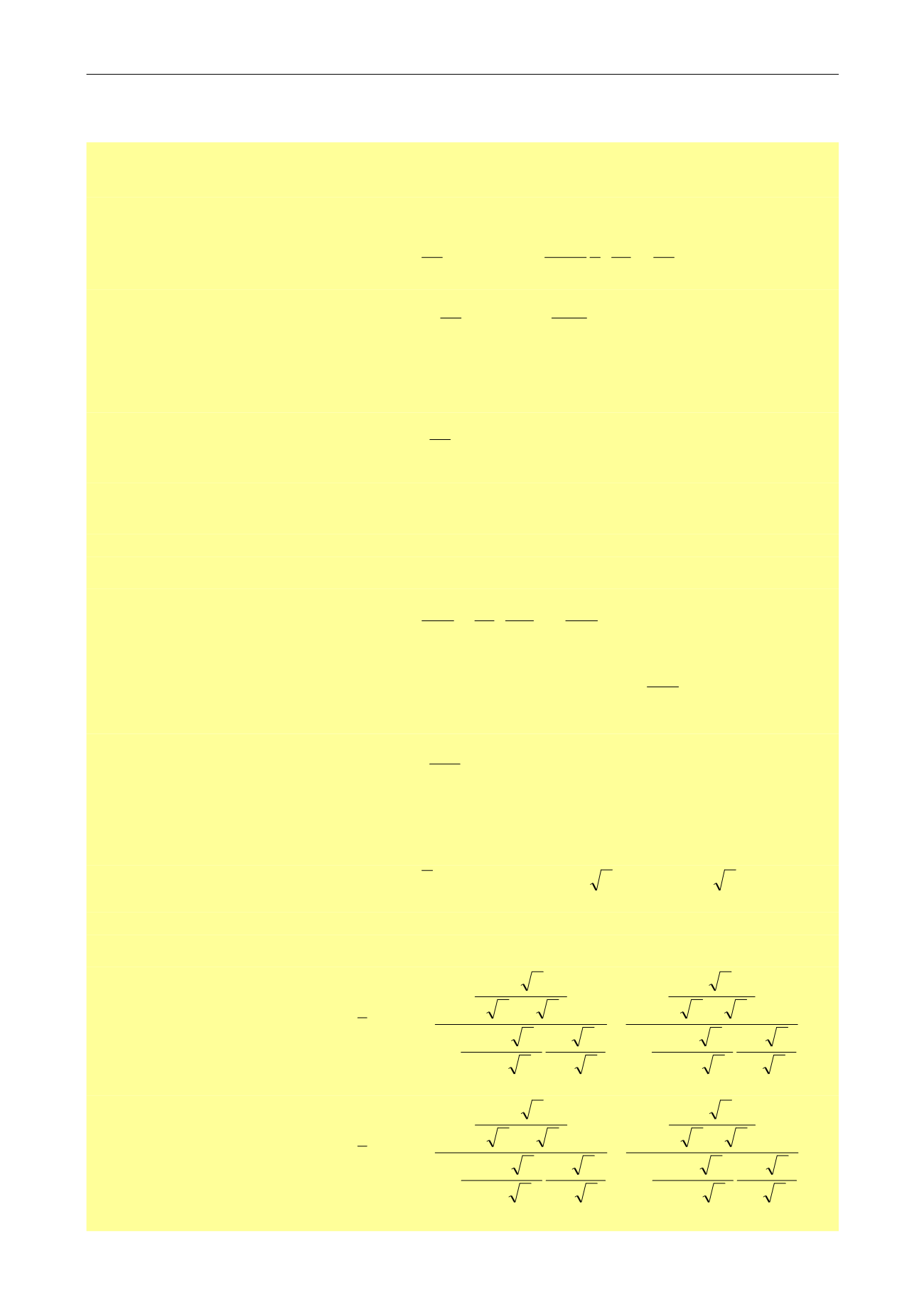
Solution of the diffusion equation:
)
( )( )
( )(
,
0
0
u r IuB u rKuA rup
D
D
D D
The terms A(u) and B(u) will be defined by the initial, inner boundary (well) and outer
boundary equations. Long story short we end up with the following solutions:
For a closed circle:
) (
) (
)
(
)
(
1
) (
) (
) (
) (
)
(
)
(
1
) (
) (
)(
1
1
1
1
1
0
1
1
1
1
1
0
u I
u K
u rK
u r I
u Iuu
u I
u K
u I
u r I
u rK
u Kuu
u K
u p
eD
eD
eD
eD
FRD
For a ct pressure circle:
) (
) (
)
(
)
(
1
) (
) (
) (
) (
)
(
)
(
1
) (
) (
)(
1
1
1
1
1
0
1
1
1
1
1
0
u I
u K
u rK
u r I
u Iuu
u I
u K
u I
u r I
u rK
u Kuu
u K
u p
eD
eD
eD
eD
FRD
















