KAPPA DDA Book v5.12

164 / 743

Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017 Chapte - p164/743
5.B Constant Wellbore storage
The simplest wellbore model is the constant wellbore storage
As introduced in the ‘Theory’ chapter, the wellbore storage introduces a time delay between
the rate we impose at the operating point (typically the choke manifold at surface) and the
sandface rate. The wellbore storage equation was introduced in the ‘Theory’ chapter:
Wellbore storage equation:
t
p
C qB qwf
sf 

 24
Not surprisingly, the constant wellbore storage model assumes that the wellbore storage factor
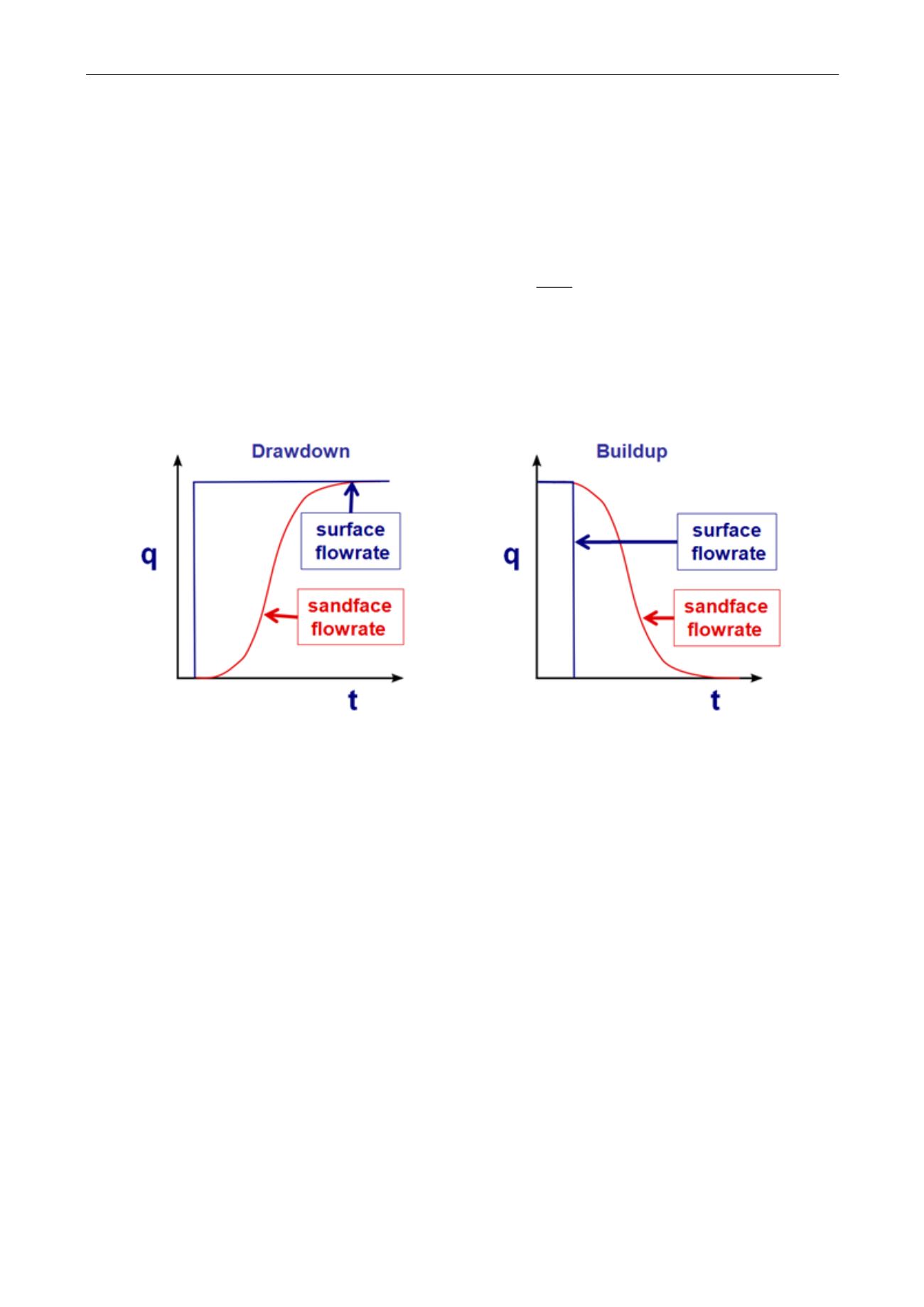
C is constant. The below figure illustrates the behavior of the sandface rate during the opening
and shut-in of a well.
Fig. 5.B.1 – Wellbore storage
5.B.1 Loglog analysis
with various constant wellbore storage constants is illustrated below. Pure wellbore
storage is characterized by the merge of both Pressure and Bourdet Derivative curves on the
same unit slope.
At a point in time, and in the absence of any other interfering behaviors, the Derivative will
leave the unit slope and transit into a hump which will stabilize into the horizontal line
corresponding to Infinite Acting Radial Flow. The form and the width of the hump is governed
by the parameter group S
Ce2 , where S is the Skin factor.
The horizontal position of the curve is only controlled by the wellbore storage coefficient C.
Taking a larger C will move the unit slope to the right, hence increase the time at which
wellbore storage will fade. More exactly, multiplying C by 10 will translate the curve to one log
cycle to the right.