
Dynamic Data Analysis – v5.12.01 - © KAPPA 1988-2017
Chapte
r 5 – W ellbore models- p168/743
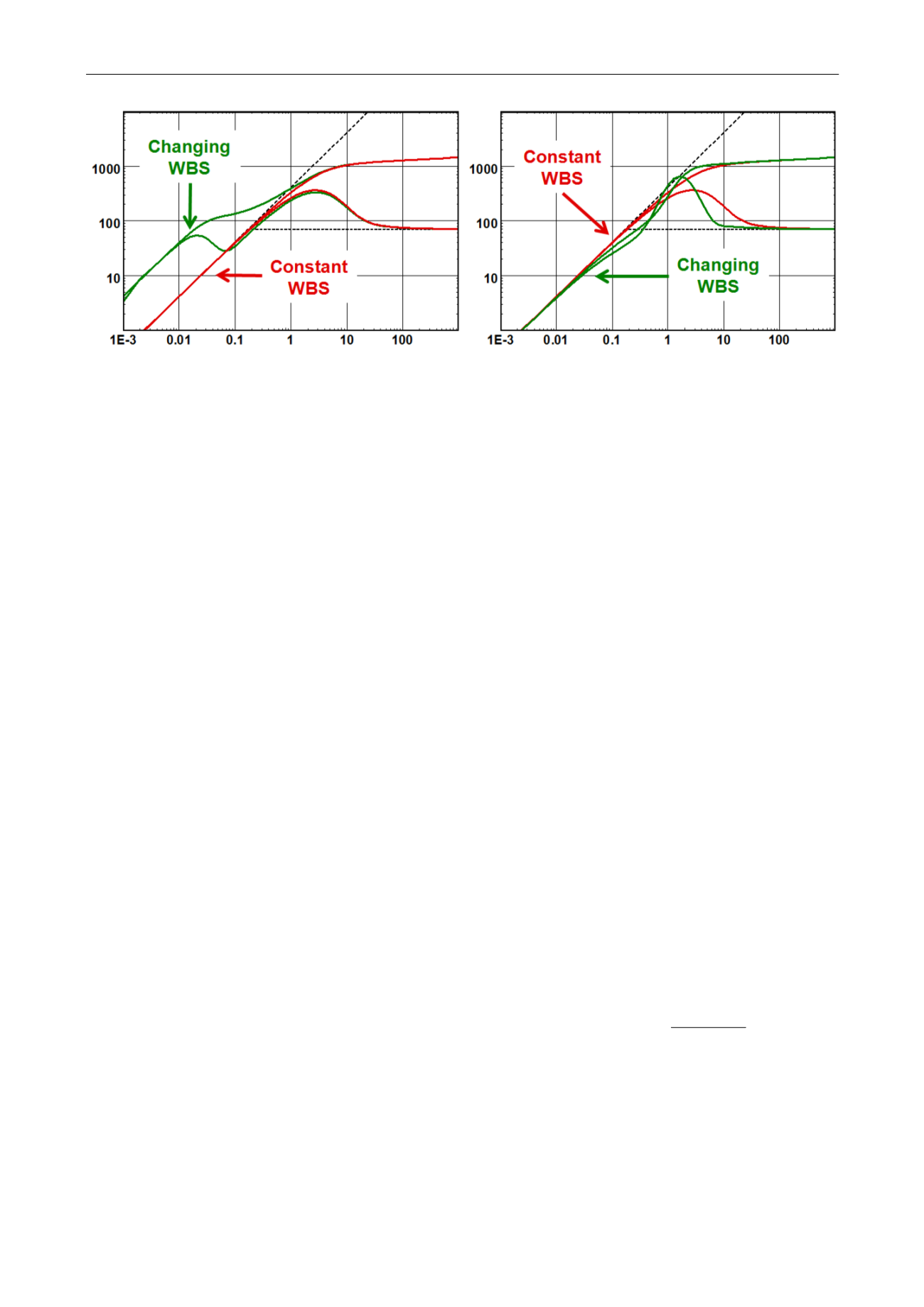
Fig. 5.C.1 – Increasing storage
Fig. 5.C.2 – Decreasing storage
In practice, the Hegeman model is sharper and has more capabilities to match real data. This
is related to the choice of transition function and does not mean that this model is physically
better. Actually it does not mean that ANY of these models are correct, and they should be
used with care for the following reasons:
The models are just transfer functions that happen to be good at matching real data. There
is no physics behind them. They may end up with an initial, final storage and transition
time that makes no physical sense.
These models are time related. There will be a wellbore storage at early time and a
wellbore storage at late time. This is not correct when the model is pressure related. In the
case of production, the real wellbore storage at early time will correspond to the storage at
late time of the build-up, and the reverse. So, the superposition of a time related solution
will be incorrect on all flow periods except the one on which the model was matched. This
aspect is often ignored and/or overlooked.
These models are ‘dangerous’ to the extent that they work beautifully to match ‘anything
that goes wrong’ at early time, even when the use of such model is not justified. They are
the early time version of the radial composite model at intermediate time. Actually,
combining changing wellbore storage and radial composite will match any rubbish data.
5.C.2
Combining pseudo-time and a constant storage model
When the pressure drawdown is large the non-constant compressibility leads to a changing
wellbore storage therefore a distortion in the early time of the loglog plot. The changes in
c
t
can also be included in the diffusion equation and pseudo-time can be used during the
extraction of the period to be analyzed.
Pseudo-time:
d pI
t t
t
wf
ps
0
where
pcp
pI
t
1
















